Question

已知抛物线x²＝4y与圆x²＋y²＝32相交于A、B两点，圆与y轴正半轴交于C点，直线l是圆的切线，交抛物线于M、N，并且切点在上．

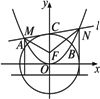
(1)求A、B、C三点的坐标；

(2)当M、N两点到抛物线焦点距离和最大时，求直线l的方程．

Answer 1

答案：
解析：

解：(1)由得A(－4，4)，B(4，4)． 　　由得C(0，4)． 　　(2)设直线l：y＝kx＋b，且直线l与抛物线交于M(x1，y1)、N(x2，y2)，抛物线x2＝4y的准线为y＝－1，焦点为F，由抛物线定义知： 　　d＝|MF|＋|NF|＝y1＋y2＋2． 　　由得y2－2(b＋2k2)y＋b2＝0， 　　则y1＋y2＝2(b＋2k2)． 　　又因为l与圆相切于，所以＝42，即k2＝－1． 　　因为直线l过C点时，b取最小值4； 　　直线l过A或B点时，b取最大值8， 　　所以b∈[4，8]． 　　所以d＝＋2b－2＝(b＋8)2－10． 　　当b＝8时，d取最大值，此时k＝±1，所以所求直线l的方程为y＝x＋8，或y＝－x＋8． 　　解析：设直线方程为y＝kx＋b，利用抛物线的定义，将点M、N到抛物线焦点的距离转化为到准线的距离，然后利用直线l与抛物线的关系，借助于直线l与圆相切，找出k与b的关系，再用配方法求出最值，从而确定直线方程．

提示：

本题的难点有两个：一是如何建立b与k的关系；二是利用图形去确定b的范围，从而求出最大值．