题目内容
某单位从一所学校招收某类特殊人才.对 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
例如,表中运动协调能力良好且逻辑思维能力一般的学生有 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为 .
.
(1)求 ,
, 的值;
的值;
(2)从参加测试的 位学生中任意抽取
位学生中任意抽取 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(3)从参加测试的 位学生中任意抽取
位学生中任意抽取 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为 ,求随机变量
,求随机变量 的分布列及其数学期望
的分布列及其数学期望 .
.
(1) ,
,  ;(2)
;(2) ;(3)所以
;(3)所以 的分布列为
的分布列为
0 1 2 



 .
.
解析试题分析:(1)求 ,
, 的值,由题意,从这
的值,由题意,从这 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为 ,而由表中数据可知,运动协调能力或逻辑思维能力优秀的学生共有
,而由表中数据可知,运动协调能力或逻辑思维能力优秀的学生共有 人,可由
人,可由 ,解出
,解出 的值,从而得
的值,从而得 的值;(2)由题意,从
的值;(2)由题意,从 人中任意抽取
人中任意抽取 人的方法数为
人的方法数为 ,而至少有一位运动协调能力或逻辑思维能力优秀的学生的对立事件是,没有取到运动协调能力或逻辑思维能力优秀的学生,而没有取到运动协调能力或逻辑思维能力优秀的学生的方法数为
,而至少有一位运动协调能力或逻辑思维能力优秀的学生的对立事件是,没有取到运动协调能力或逻辑思维能力优秀的学生,而没有取到运动协调能力或逻辑思维能力优秀的学生的方法数为 ,由古典概型,可求出没有运动协调能力或逻辑思维能力优秀的学生的概率,从而得所求的概率;(3)由题意得
,由古典概型,可求出没有运动协调能力或逻辑思维能力优秀的学生的概率,从而得所求的概率;(3)由题意得 的可能取值为
的可能取值为 ,由古典概型,分别求出它们的概率,得随机变量
,由古典概型,分别求出它们的概率,得随机变量 的分布列,从而得数学期望
的分布列,从而得数学期望 .
.
试题解析:(I)设事件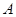 :从
:从 位学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生.由题意可知,运动协调能力或逻辑思维能力优秀的学生共有
位学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生.由题意可知,运动协调能力或逻辑思维能力优秀的学生共有 人.
人.
则 .解得
.解得  .所以
.所以 . 4分
. 4分
(2)设事件 :从
:从 人中任意抽取
人中任意抽取 人,至少有一位运动协调能力或逻辑思维能力优秀的学生.
人,至少有一位运动协调能力或逻辑思维能力优秀的学生.
由题意可知,至少有一项能力测试优秀的学生共有 人.
人.
则 . 7分
. 7分
(3) 的可能取值为
的可能取值为 ,
, ,
, .
. 位学生中运动协调能力或逻辑思维能力优秀的学生人数为
位学生中运动协调能力或逻辑思维能力优秀的学生人数为 人.
人.
所以 ,
, ,
, .
.
所以 的分布列为
的分布列为
所以,
0 1 2 



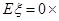





 . 13分
. 13分
考点:古典概型,分布列,数学期望.

 .
.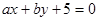 与圆
与圆 相切的概率;
相切的概率; 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原 个元件,寿命为
个元件,寿命为 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为 ,一个寿命为
,一个寿命为 ”的概率.
”的概率. 、
、 两个盒子中分别装有标记为
两个盒子中分别装有标记为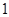 ,
, ,
, ,
, 的大小相同的四个小球,甲从
的大小相同的四个小球,甲从 表示事件“甲抽到标号为
表示事件“甲抽到标号为 的小球,乙抽到标号为
的小球,乙抽到标号为 的小球”,试写出所有可能的事件;
的小球”,试写出所有可能的事件; ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数. 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 ,除以3的余数为
,除以3的余数为
 为事件
为事件 ,事件
,事件 为事件
为事件 ,判断事件
,判断事件