题目内容
7.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,8,13,….该数列的特点是:前两个数都是1,从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列{an}称为“斐波那契数列”,则(a1a3-a${\;}_{2}^{2}$)(a2a4-a${\;}_{3}^{2}$)(a3a5-a${\;}_{4}^{2}$)…(a2015a2017-a${\;}_{2016}^{2}$)=( )| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
分析 利用a1a3-a${\;}_{2}^{2}$=1×2-12=1,a2a4-a${\;}_{3}^{2}$=1×3-22=-1,a3a5-a${\;}_{4}^{2}$=2×5-32=1,…,a2015a2017-a${\;}_{2016}^{2}$=1.即可得出.
解答 解:∵a1a3-a${\;}_{2}^{2}$=1×2-12=1,a2a4-a${\;}_{3}^{2}$=1×3-22=-1,
a3a5-a${\;}_{4}^{2}$=2×5-32=1,…,a2015a2017-a${\;}_{2016}^{2}$=1.
∴(a1a3-a${\;}_{2}^{2}$)(a2a4-a${\;}_{3}^{2}$)(a3a5-a${\;}_{4}^{2}$)…(a2015a2017-a${\;}_{2016}^{2}$)=11008×(-1)1007=-1.
故选:B.
点评 本题考查了斐波那契数列的性质及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.设z是复数,则下列命题中的假命题是( )
| A. | 若z是纯虚数,则z2<0 | B. | 若z是虚数,则z2≥0 | ||
| C. | 若z2≥0,则z是实数 | D. | 若z2<0,则z是虚数 |
2.某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.
9.已知函数f(x)=$\left\{\begin{array}{l}{1-|x|,x≤1}\\{(x-1)^{2},x>1}\end{array}\right.$,若函数y=f(x)+f(1-x)-m恰有4个零点,则m的取值范围是( )
| A. | ($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{3}{4}$) | C. | (0,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
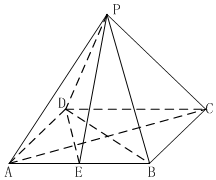 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.