题目内容
13.已知sinα+cosα=$\frac{1}{3}$,0<α<π,求:(1)sinα-cosα的值,(2)sin3α-cos3α的值.分析 (1)由已知利用同角三角函数关系式得2sinαcosα=-$\frac{8}{9}$,sinα>0,cosα<0,由此能求出sinα-cosα.
(2)由sin3α-cos3α=(sinα-cosα)(sin2α+sinαcosα+cos2α),利用同角三角函数关系式能求出结果.
解答 解:(1)∵sinα+cosα=$\frac{1}{3}$,0<α<π,
∴1+2sinαcosα=$\frac{1}{9}$,
∴2sinαcosα=-$\frac{8}{9}$,∴sinα>0,cosα<0,
∴(sinα-cosα)2=1-2sinαcosα=$\frac{17}{9}$,
∴sinα-cosα=$\frac{\sqrt{17}}{3}$.
(2)sin3α-cos3α
=(sinα-cosα)(sin2α+sinαcosα+cos2α)
=$\frac{\sqrt{17}}{3}$(1-$\frac{4}{9}$)
=$\frac{5\sqrt{17}}{27}$.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意同角三角函数性质的合理运用.

练习册系列答案
相关题目
18.复数z=$\frac{3+i}{1-i}$(其中i为虚数单位)的虚部是( )
| A. | -1 | B. | -i | C. | 2i | D. | 2 |
 如图所示,在△ABC中,D,E,F分别是AB,BC,CA的中点,求证:
如图所示,在△ABC中,D,E,F分别是AB,BC,CA的中点,求证: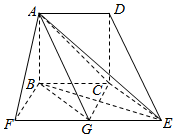 如图,四边形ABCD为正方形,AB⊥平面BCEF,G是EF的中点,BC∥EF,BC=CE=$\frac{1}{2}$EF.
如图,四边形ABCD为正方形,AB⊥平面BCEF,G是EF的中点,BC∥EF,BC=CE=$\frac{1}{2}$EF.