题目内容
(2013•宝山区一模)设A(x1,y1),B(x2,y2)是平面直角坐标系上的两点,定义点A到点B的曼哈顿距离L(A,B)=|x1-x2|+|y1-y2|.若点A(-1,1),B在y2=x上,则L(A,B)的最小值为
.
| 7 |
| 4 |
| 7 |
| 4 |
分析:分析可知,使L(A,B)取最小值的点应在原点或第一象限,设出抛物线上点的坐标,然后写出L(A,B)=|y02+1|+|y0-1|.分类讨论点B的纵坐标后可求得L(A,B)的最小值.
解答:解:如图,
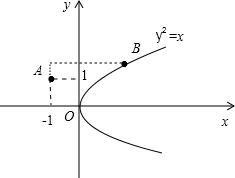
因为A在第二象限,根据抛物线的对称性,要使抛物线上的点B与A点的曼哈顿距离最小,则B在第一象限(或原点).
设B(y02,y0),
则L(A,B)=|y02+1|+|y0-1|
当0≤y0≤1时,
L(A,B)=y02+1+1-y0
=y02-y0+2
=(y0-
)2+
,
所以,当y0=
时,L(A,B)有最小值
.
当y0>1时,
L(A,B)=y02+1+y0-1
=y02+y0
=(y0+
)2-
>(1+
)2-
=2.
综上,L(A,B)的最小值为
.
故答案为
.

因为A在第二象限,根据抛物线的对称性,要使抛物线上的点B与A点的曼哈顿距离最小,则B在第一象限(或原点).
设B(y02,y0),
则L(A,B)=|y02+1|+|y0-1|
当0≤y0≤1时,
L(A,B)=y02+1+1-y0
=y02-y0+2
=(y0-
| 1 |
| 2 |
| 7 |
| 4 |
所以,当y0=
| 1 |
| 2 |
| 7 |
| 4 |
当y0>1时,
L(A,B)=y02+1+y0-1
=y02+y0
=(y0+
| 1 |
| 2 |
| 1 |
| 4 |
>(1+
| 1 |
| 2 |
| 1 |
| 4 |
综上,L(A,B)的最小值为
| 7 |
| 4 |
故答案为
| 7 |
| 4 |
点评:本题考查了新定义下的两点间的距离公式,考查了数形结合的解题思想和分类讨论思想,解答的关键是设出B点的坐标,此题是中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目