题目内容
设x1,x2(x1≠x2)是函数f(x)=ax3+bx2﹣a2x(a>0)的两个极值点.
(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若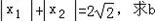 的最大值;
的最大值;
(3)设函数g(x)=f(x)﹣a(x﹣x1),x∈(x1,x2),当x2=a时,求证: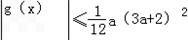 .
.
(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若
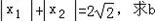 的最大值;
的最大值;(3)设函数g(x)=f(x)﹣a(x﹣x1),x∈(x1,x2),当x2=a时,求证:
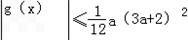 .
.解:(1)∵f(x)=ax3+bx2﹣a2x(a>0),
∴f'(x)=3ax2+2bx﹣a2,(a>0),
依题意有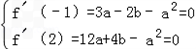 ,(a>0)
,(a>0)
解得a=6,b=﹣9,
∴f(x)=6x3﹣9x2﹣36x.
(2)∵f'(x)=3ax2+2bx﹣a2,(a>0),
依题意,x1,x2是方程f'(x)=0的两个根,且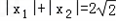 ,
,
∴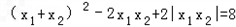 ,
,
∴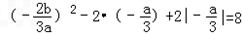 ,
,
∴b2=3a2(6﹣a),
∵b2≥0,
∴0<a≤6,
设p(a)=3a2(6﹣a),则p'(a)=﹣9a2+36a,
由p'(a)>0,得0<a<4,
由p'(a)<0,得a>4,
即:函数p(a)在区间(0,4]上是增函数,在[4,6]上是减函数.
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是4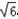
∴b的最大值是4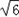 .
.
(3)证明:∵x1,x2是方程f'(x)=0的两根,
∴f'(x)=3a(x﹣x1)(x﹣x2),
∵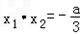 ,x2=a,
,x2=a,
∴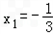 ,
,
∴|g(x)|=|3a(x+ )[3(x﹣a)﹣1],
)[3(x﹣a)﹣1],
∵x1<x<x2,即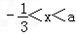 ,
,
∴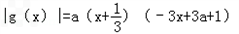 ,
,
∴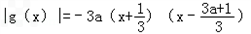 =﹣3a
=﹣3a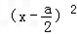 +
+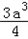 +
+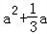
≤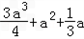 =
=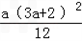 ,
,
∴|g(x)|≤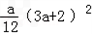 成立.
成立.
∴f'(x)=3ax2+2bx﹣a2,(a>0),
依题意有
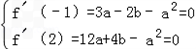 ,(a>0)
,(a>0)解得a=6,b=﹣9,
∴f(x)=6x3﹣9x2﹣36x.
(2)∵f'(x)=3ax2+2bx﹣a2,(a>0),
依题意,x1,x2是方程f'(x)=0的两个根,且
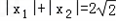 ,
,∴
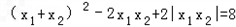 ,
,∴
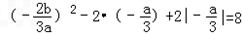 ,
,∴b2=3a2(6﹣a),
∵b2≥0,
∴0<a≤6,
设p(a)=3a2(6﹣a),则p'(a)=﹣9a2+36a,
由p'(a)>0,得0<a<4,
由p'(a)<0,得a>4,
即:函数p(a)在区间(0,4]上是增函数,在[4,6]上是减函数.
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是4
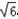
∴b的最大值是4
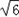 .
.(3)证明:∵x1,x2是方程f'(x)=0的两根,
∴f'(x)=3a(x﹣x1)(x﹣x2),
∵
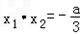 ,x2=a,
,x2=a,∴
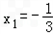 ,
,∴|g(x)|=|3a(x+
 )[3(x﹣a)﹣1],
)[3(x﹣a)﹣1],∵x1<x<x2,即
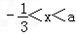 ,
,∴
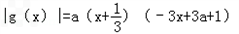 ,
,∴
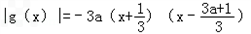 =﹣3a
=﹣3a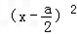 +
+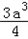 +
+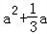
≤
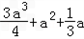 =
=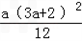 ,
,∴|g(x)|≤
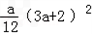 成立.
成立.
练习册系列答案
相关题目