题目内容
若直线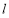 经过点
经过点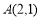 ,且与直线
,且与直线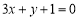 垂直,则直线
垂直,则直线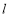 的方程为 .
的方程为 .
 .
.
【解析】
试题分析:当斜率存在时,两条直线垂直,斜率之积为-1,所以直线l的斜率是 ,再利用点斜式即可.
,再利用点斜式即可.
考点:(1)两条直线垂直的条件;(2)直线方程.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
题目内容
若直线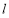 经过点
经过点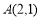 ,且与直线
,且与直线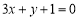 垂直,则直线
垂直,则直线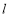 的方程为 .
的方程为 .
 .
.
【解析】
试题分析:当斜率存在时,两条直线垂直,斜率之积为-1,所以直线l的斜率是 ,再利用点斜式即可.
,再利用点斜式即可.
考点:(1)两条直线垂直的条件;(2)直线方程.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案