题目内容
已知点 ,又P(x,y)是曲线
,又P(x,y)是曲线 上的点,则( )
上的点,则( )A.|PF1|+|PF2|=4
B.|PF1|+|PF2|<4
C.|PF1|+|PF2|≤4
D.|PF1|+|PF2|≥4
【答案】分析:化简曲线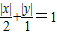 得直线
得直线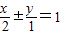 和直线
和直线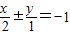 ,所得的直线都与椭圆
,所得的直线都与椭圆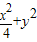 =1相切.由此结合椭圆的定义加以运算,即可得到|PF1|+|PF2|≥4,从而得到本题答案.
=1相切.由此结合椭圆的定义加以运算,即可得到|PF1|+|PF2|≥4,从而得到本题答案.
解答:解:当|PF1|+|PF2|=4时,
根据椭圆的定义得到满足条件的点在椭圆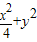 =1上
=1上
化简曲线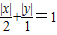 ,可得直线
,可得直线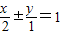 和直线
和直线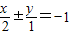
∵直线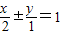 和直线
和直线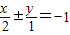 与椭圆
与椭圆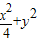 =1的位置关系都是相切
=1的位置关系都是相切
∴当P(x,y)是曲线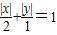 上的点时,点P在椭圆上或在椭圆外,
上的点时,点P在椭圆上或在椭圆外,
因此满足|PF1|+|PF2|≥4
故选:D
点评:本题给出曲线上的动点,判断该点与椭圆的位置关系,着重考查了椭圆的定义与标准方程、直线与圆锥曲线的位置关系等知识,属于基础题.
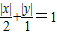 得直线
得直线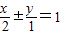 和直线
和直线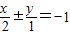 ,所得的直线都与椭圆
,所得的直线都与椭圆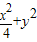 =1相切.由此结合椭圆的定义加以运算,即可得到|PF1|+|PF2|≥4,从而得到本题答案.
=1相切.由此结合椭圆的定义加以运算,即可得到|PF1|+|PF2|≥4,从而得到本题答案.解答:解:当|PF1|+|PF2|=4时,
根据椭圆的定义得到满足条件的点在椭圆
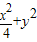 =1上
=1上化简曲线
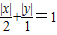 ,可得直线
,可得直线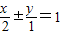 和直线
和直线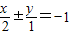
∵直线
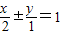 和直线
和直线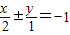 与椭圆
与椭圆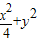 =1的位置关系都是相切
=1的位置关系都是相切∴当P(x,y)是曲线
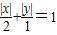 上的点时,点P在椭圆上或在椭圆外,
上的点时,点P在椭圆上或在椭圆外,因此满足|PF1|+|PF2|≥4
故选:D
点评:本题给出曲线上的动点,判断该点与椭圆的位置关系,着重考查了椭圆的定义与标准方程、直线与圆锥曲线的位置关系等知识,属于基础题.

练习册系列答案
相关题目