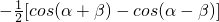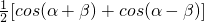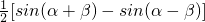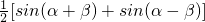题目内容
利用积化和差公式化简sinαsin(
-β)的结果为( )
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
分析:先把sin(
-β)利用诱导公式化简后,把sinαcosβ利用积化和差公式化简可得值.
| π |
| 2 |
解答:解:sinαsin(
-β)=sinαcosβ=
[sin(α+β)+sin(α-β)]
故选D
| π |
| 2 |
| 1 |
| 2 |
故选D
点评:考查学生会利用诱导公式化简求值,掌握积化和差的运算公式.此题比较简单.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
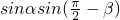 的结果为
的结果为