题目内容
(1)设α为锐角,试比较sin2α和sin(α+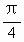 )的大小;
)的大小;
(2)已知θ∈(0,2π)且sinθcos2θ>0,求θ的范围.
答案:
解析:
提示:
解析:
|
解 (1)分别画出y=sin2α(0<α<
(2)解法1 (Ⅰ) 解法2 转化为sinθ(sinθ- |
提示:
|
注 (1)的比较大小,可用作差法,然后和差化积解之. |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 )和y=sin(α+
)和y=sin(α+ )(0<α<
)(0<α< ).
).
 由cos2θ>0
由cos2θ>0 <2θ<2π或0≤2θ<
<2θ<2π或0≤2θ< (舍)或
(舍)或 <θ<π或0≤θ<
<θ<π或0≤θ< (舍去θ=0),它们都满足sinθ>0.(Ⅱ)
(舍去θ=0),它们都满足sinθ>0.(Ⅱ) 仿(Ⅰ)
仿(Ⅰ) ,即
,即 .
.  )(sinθ+
)(sinθ+ ∪
∪ .
.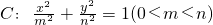 的离心率为
的离心率为 ,且经过点
,且经过点 .
.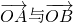 的夹角为锐角,试求k的取值范围.
的夹角为锐角,试求k的取值范围.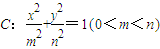 的离心率为
的离心率为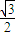 ,且经过点
,且经过点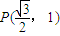 .
.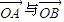 的夹角为锐角,试求k的取值范围.
的夹角为锐角,试求k的取值范围.