题目内容
12．圆（x-1）2+（y+2）2=20上到直线x-2y=0的距离为$\sqrt{5}$的点的个数是3．分析 先求出圆心到直线x-2y=0的距离d的值，再将d与半径对比，从而得出结论．
解答 解：圆（x-1）2+（y+2）2=20的圆心坐标（1，-2），半径2$\sqrt{5}$，
由点到直线的距离公式得圆心到直线x-2y=0的距离d=$\frac{|1+4|}{\sqrt{1+4}}$=$\sqrt{5}$，
所以圆上到直线x-2y=0的距离为$\sqrt{5}$的点有3个，
故答案为：3．
点评 本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
3．若直线（m+3）x+（m2-3）y-2m=0在x轴上的截距是1，则实数m的值等于（ ）
| A． | -1 | B． | 1 | C． | -3 | D． | 3 |
20．（1+$\frac{1}{2}$x）5的展开式中的第三项的系数为（ ）
| A． | 5 | B． | $\frac{5}{2}$ | C． | $\frac{5}{4}$ | D． | $\frac{5}{8}$ |
7．在椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1中，过点P（1，1）的弦被点P平分，则此弦所在的直线方程为（ ）
| A． | x+2y-3=0 | B． | x-2y-3=0 | C． | x+2y+3=0 | D． | x-2y+3=0 |
4．数列{an}中，a1∈Z，an+1=an+log2（1-$\frac{1}{n+1}$），则使{an}为整数的n的取值可能是（ ）
| A． | 1022 | B． | 1023 | C． | 1024 | D． | 1025 |
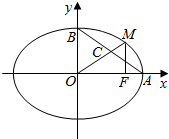如图所示，A，B分别是椭圆的右、上顶点，C是AB的三等分点（靠近点B），F为椭圆的右焦点，OC的延长线交椭圆于点M，且MF⊥OA，则椭圆的离心率为$\frac{\sqrt{5}}{5}$．