题目内容
已知函数
(1)解不等式 ;
;
(2)若 ,且
,且 ,求证:
,求证: .
.
(Ⅰ)f(x)+f(x+4)=|x-1|+|x+3|=
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3.
所以不等式f(x)≤4的解集为{x|x≤-5,或x≥3}. …………5分
(Ⅱ)f(ab)>|a|f( )即|ab-1|>|a-b|. …………6分
)即|ab-1|>|a-b|. …………6分
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|.
故所证不等式成立.

练习册系列答案
相关题目
某同学用“五点法”画函数
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
| 0 |
|
|
|
|
|
|
|
| |||
|
| 0 | 5 |
| 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数 的解析式;
的解析式;
(Ⅱ)将 图象上所有点向左平行移动
图象上所有点向左平行移动 个单位长度,得到
个单位长度,得到 图象,求
图象,求
 的图象离原点
的图象离原点 最近的对称中心.
最近的对称中心.










 ,
,
 上两点
上两点 和
和 ,其中
,其中 .过
.过 的直线
的直线 与
与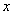 轴交于
轴交于 ,那么( )
,那么( ) 成等差数列 B.
成等差数列 B. 成等差数列 D.
成等差数列 D. 正方体截去一半(如图6所示)得到如图7所示的几何体,点
正方体截去一半(如图6所示)得到如图7所示的几何体,点 ,
, 分别是
分别是 ,
, 的中点.
的中点. (1)证明:
(1)证明: ;
; (2)求三棱锥
(2)求三棱锥 的体积.
的体积.
 B.
B.  C.
C.  D.
D. 
 ,
, ,…,
,…, 中最大的是()
中最大的是() C.
C.  D.
D.  满足
满足 ,且a5·a6=2,则log2a1+ log2a2+…+ log2a10=( )A.2 B.4 C.5 D.25
,且a5·a6=2,则log2a1+ log2a2+…+ log2a10=( )A.2 B.4 C.5 D.25 的值域是 ( )
的值域是 ( ) B.
B.  C.
C.  D.
D. 