Question

（本题满分14分）

已知函数，是方程f(x)=0的两个根，是f(x)的导数.

设，（n=1,2,……）

 （1）求的值；

 （2）证明：对任意的正整数n，都有>a；

（3）记（n=1,2,……），求数列{b_n}的前n项和S_n。

Answer 1

(-∞,         ]∪[1, +∞)

解析:

(1)解方程x²+x-1=0得x=      

由?知?=,β=      

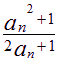
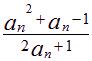
(2) f’ (x)=2x+1

         =     -                =            

下面我们用数学归纳法来证明该结论成立

①当n=1时，a₁=1<=?成立，

②假设n=k(k≥1, k∈N*)时，结论也成立，即a_k<成立，

③那么当n=k+1时，

==-+<-+=+=

        

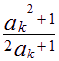这就是说，当n=k+1时，结论也成立，故对于任意的正整数n，都有a_n<

(3)

=   =       =

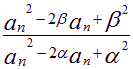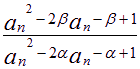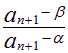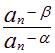=()²

由题意知a_n>,那么有a_n>β，于是对上式两边取对数得

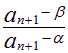ln=ln(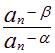)²=2 ln()

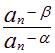即数列{b_n}为首项为b₁= ln(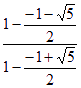)=2ln(       )，公比为2的等比数列。

故其前n项和

 

S_n=2ln(       )       =2ln(       )(2ⁿ -1).