题目内容
对于实数 和
和 ,定义运算“*”:
,定义运算“*”: ,设
,设 ,且关于x的方程
,且关于x的方程 恰有三个互不相等的实数根,则实数
恰有三个互不相等的实数根,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析:由 2x-1≤x-1 可得 x≤0,由 2x-1>x-1 可得 x>0.
∴根据题意得f(x)= .
.
即 f(x)= ,
,
画出函数的图象,从图象上观察当关于x的方程为f(x)=a(a∈R)恰有三个互不相等的实数根时,
函数的图象和直线y=a有三个不同的交点.
再根据函数的极大值为f(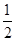 )=
)= ,
,
可得a的取值范围是(0, ),故选 A.
),故选 A.
考点:本题主要考查学习能力,分段函数的概念,二次函数的图象和性质。
点评:中档题,关键是理解新定义内容,转化得到分段函数的解析式,利用二次函数的图象和性质,研究方程根的情况。

练习册系列答案
相关题目
“
 ”是“
”是“
 ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列函数中,在其定义域内既是奇函数又是减函数的是
A. | B. | C. | D. |
三个数 的大小关系为( )
的大小关系为( )
A. | B. |
C. | D. |
设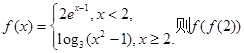 的值为 ( )
的值为 ( )
| A.0 | B.1 | C.2 | D.3 |
设 ,
, ,
, (其中
(其中 为自然对数的底数),则
为自然对数的底数),则
A. | B. | C.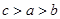 | D. |
若函数 在区间
在区间 上的最大值是最小值的
上的最大值是最小值的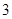 倍,则
倍,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知定义在R上的函数 满足
满足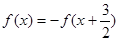 且
且 ,
, 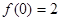 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
 为奇函数,且函数
为奇函数,且函数 的图像关于点
的图像关于点 对称,点
对称,点 在直线
在直线 ,则
,则 的最小值是( )
的最小值是( )


