题目内容
若函数 为奇函数,且函数
为奇函数,且函数 的图像关于点
的图像关于点 对称,点
对称,点 在直线
在直线 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
C
解析试题分析:函数y=f(x+2)-2向右平移2个单位,再向上平移2个单位可得到函数y=f(x)的图象,
又∵函数y=f(x+2)-2为奇函数,对称中心为(0,0),
∴y=f(x)的对称中心为(2,2)即a=b=2,故ax+by=2x+2y≥2
 ,故选C.
,故选C.
考点:函数的奇偶性,函数图象的平移变换,均值定理的应用。
点评:中档题,本题综合性较强,将函数的奇偶性、图象的对称性、图象的变换与函数的最值结合在一起,运用均值定理达到目的。

练习册系列答案
相关题目
已知函数 则
则 的值是
的值是
| A.10 | B. | C.-2 | D.-5 |
已知函数 下列命题正确的是 ( )
下列命题正确的是 ( )
A.若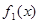 是增函数, 是增函数, 是减函数,则 是减函数,则 存在最大值 存在最大值 |
B.若 存在最大值,则 存在最大值,则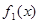 是增函数, 是增函数, 是减函数 是减函数 |
C.若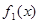 , , 均为减函数,则 均为减函数,则 是减函数 是减函数 |
D.若 是减函数,则 是减函数,则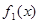 , , 均为减函数 均为减函数 |
下列对函数 的性质描述正确的是( )
的性质描述正确的是( )
| A.偶函数,先减后增 | B.偶函数,先增后减 |
| C.奇函数,减函数 | D.偶函数,减函数 |
设函数 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. |
C. | D. |
若方程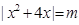 有实数根,则所有实数根的和可能为
有实数根,则所有实数根的和可能为
| A.-2,-4,-6 | B.-4,-5,-6 | C.-3,-4,-5 | D.-4,-6,-8 |
不等式2x2-x-1>0的解集是
A. | B.(1, + ) ) |
C.(- ,1)∪(2,+ ,1)∪(2,+ ) ) | D. |
函数 的单调减区间为 ( )
的单调减区间为 ( )
A. | B.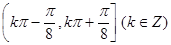 |
C. | D. |
 和
和 ,定义运算“*”:
,定义运算“*”: ,设
,设 ,且关于x的方程
,且关于x的方程 恰有三个互不相等的实数根,则实数
恰有三个互不相等的实数根,则实数


