题目内容
给出下列命题:
①ambn=(ab)m+n;
②若f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;
③a<0是方程ax2+2x+1=0有一个负实数根的充分不必要条件;
④设有四个函数y=x-1,y=x3,y=x
,y=x4,其中y随x增大而增大的函数有3个.
其中正确命题的个数为( )
①ambn=(ab)m+n;
②若f(x)是奇函数,则f(x-1)的图象关于点A(1,0)对称;
③a<0是方程ax2+2x+1=0有一个负实数根的充分不必要条件;
④设有四个函数y=x-1,y=x3,y=x
| 1 |
| 2 |
其中正确命题的个数为( )
分析:①根据指数幂的运算法则判断.②利用函数奇偶性的性质,以及函数平移关系判断.③利用充分条件和必要条件的定义进行判断.④利用增函数的定义判断.
解答:解:①由指数幂的运算法则知(ab)m+n=am+nbm+n,所以①错误.
②若f(x)是奇函数,则函数f(x)关于(0,0)对称,将函数f(x)向右平移一个单调,得到f(x-1),此时函数f(x-1)关于(1,0)对称,所以②正确.
③当a=0时,方程等价为2x+1=0,解得x=-
<0.此时满足条件.当a≠0,若方程有两个互异的实根,则两根之积为
<0,解得a<0.若方程有两个负实根,则
,解得0<a≤1,综上a≤1,所以a<0是方程ax2+2x+1=0有一个负实数根的充分不必要条件,所以③正确.
④函数y=x-1,y=x4在定义域内不是单调函数,y=x
,y=x3在定义域内单调递增函数,所以④错误.
故选:B.
②若f(x)是奇函数,则函数f(x)关于(0,0)对称,将函数f(x)向右平移一个单调,得到f(x-1),此时函数f(x-1)关于(1,0)对称,所以②正确.
③当a=0时,方程等价为2x+1=0,解得x=-
| 1 |
| 2 |
| 1 |
| a |
|
④函数y=x-1,y=x4在定义域内不是单调函数,y=x
| 1 |
| 2 |
故选:B.
点评:本题主要考查函数性质 的综合应用,要求熟练掌握相关的函数性质.

练习册系列答案
相关题目
 中直线AM与x轴交于点N(n,0),设f(m)=n.
中直线AM与x轴交于点N(n,0),设f(m)=n.

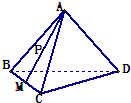 在正四面体A-BCD中,棱长为4,M是BC的中点,P在线段AM上运动(P不与A、M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥面AMD;②Q点一定在直线DM上 ③VC-AMD=4
在正四面体A-BCD中,棱长为4,M是BC的中点,P在线段AM上运动(P不与A、M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥面AMD;②Q点一定在直线DM上 ③VC-AMD=4