题目内容
对任意两个非零的平面向量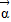 和
和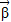 ,定义
,定义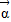 •
•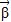 =
=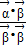 .若平面向量
.若平面向量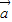 ,
,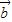 满足|
满足|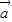 |≥|
|≥|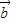 |>0,
|>0,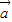 与
与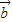 的夹角θ∈(0,
的夹角θ∈(0,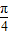 ),且
),且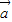 •
•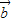 和
和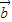 •
•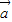 都在集合{
都在集合{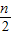 |n∈Z}中,则
|n∈Z}中,则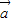 •
•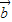 =( )
=( )A.

B.1
C.

D.

【答案】分析:由题意可得 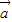 •
•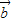 =
=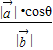 =
=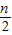 ,同理可得
,同理可得 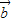 •
•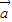 =
=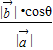 =
=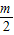 ,故有 n≥m 且 m、n∈z.再由 cos2θ=
,故有 n≥m 且 m、n∈z.再由 cos2θ=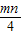 ,
,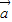 与
与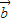 的夹角θ∈(0,
的夹角θ∈(0,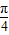 ),可得
),可得
cos2θ∈( ,1),即
,1),即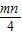 ∈(
∈( ,1),由此求得 n=3,m=1,从而得到
,1),由此求得 n=3,m=1,从而得到 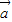 •
•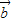 =
=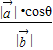 =
=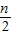 的值.
的值.
解答:解:由题意可得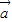 •
•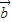 =
=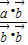 =
=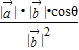 =
=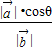 =
=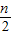 .
.
同理可得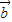 •
•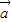 =
=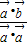 =
=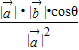 =
=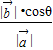 =
=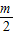 .
.
由于|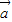 |≥|
|≥|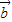 |>0,∴n≥m 且 m、n∈z.
|>0,∴n≥m 且 m、n∈z.
∴cos2θ=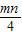 .再由
.再由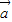 与
与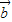 的夹角θ∈(0,
的夹角θ∈(0,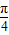 ),可得 cos2θ∈(
),可得 cos2θ∈( ,1),即
,1),即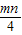 ∈(
∈( ,1).
,1).
故有 n=3,m=1,∴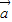 •
•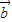 =
=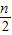 =
= ,
,
故选C.
点评:本题主要考查两个向量的数量积的定义,得到 n≥m 且 m、n∈z,且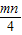 ∈(
∈( ,1),是解题的关键,属于中档题.
,1),是解题的关键,属于中档题.
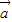 •
•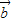 =
=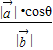 =
=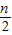 ,同理可得
,同理可得 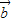 •
•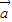 =
=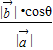 =
=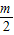 ,故有 n≥m 且 m、n∈z.再由 cos2θ=
,故有 n≥m 且 m、n∈z.再由 cos2θ=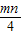 ,
,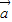 与
与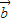 的夹角θ∈(0,
的夹角θ∈(0,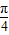 ),可得
),可得cos2θ∈(
 ,1),即
,1),即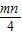 ∈(
∈( ,1),由此求得 n=3,m=1,从而得到
,1),由此求得 n=3,m=1,从而得到 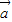 •
•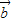 =
=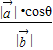 =
=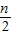 的值.
的值.解答:解:由题意可得
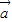 •
•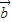 =
=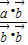 =
=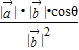 =
=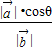 =
=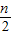 .
.同理可得
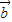 •
•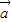 =
=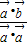 =
=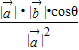 =
=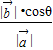 =
=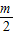 .
.由于|
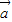 |≥|
|≥|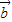 |>0,∴n≥m 且 m、n∈z.
|>0,∴n≥m 且 m、n∈z.∴cos2θ=
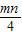 .再由
.再由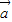 与
与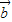 的夹角θ∈(0,
的夹角θ∈(0,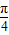 ),可得 cos2θ∈(
),可得 cos2θ∈( ,1),即
,1),即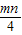 ∈(
∈( ,1).
,1).故有 n=3,m=1,∴
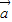 •
•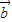 =
=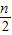 =
= ,
,故选C.
点评:本题主要考查两个向量的数量积的定义,得到 n≥m 且 m、n∈z,且
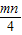 ∈(
∈( ,1),是解题的关键,属于中档题.
,1),是解题的关键,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目