题目内容
已知函数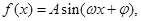
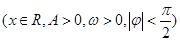 的部分图象如图所示:
的部分图象如图所示: 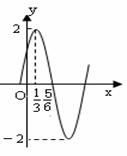
(Ⅰ)试确定 的解析式;
的解析式;
(Ⅱ)若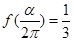 , 求
, 求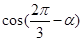 的值.
的值.
(Ⅰ)f(x)=2sin(πx+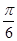 ) (x∈R) (Ⅱ)
) (x∈R) (Ⅱ)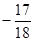
解析试题分析:(Ⅰ)由图象可知A="2," 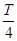 =
= 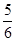 -
-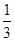 =
=  , ∴T=2,ω=
, ∴T=2,ω= 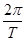 =π
=π
将点(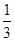 , 2)代入y=2sin(πx+j), 得 sin(
, 2)代入y=2sin(πx+j), 得 sin(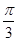 +j)="1," 又|j| <
+j)="1," 又|j| < 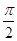
所以j =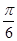 . 故所求解析式为f(x)=2sin(πx+
. 故所求解析式为f(x)=2sin(πx+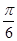 ) (x∈R)
) (x∈R)
(Ⅱ)∵f(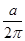 ) =
) = 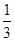 , ∴2sin(
, ∴2sin(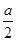 +
+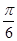 ) =
) = 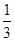 , 即, sin(
, 即, sin(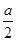 +
+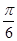 ) =
) = 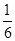
∴cos(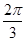 -a)=cos[π-2(
-a)=cos[π-2(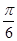 +
+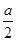 )] =-cos2(
)] =-cos2(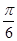 +
+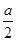 )=2sin2(
)=2sin2(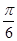 +
+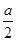 )-1 =
)-1 =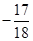
考点:由y= A sin(ωx+φ)的部分图象确定其解析式.
点评:本题考查由y="A" sin(ωx+φ)的部分图象确定其解析式,突出考查特值法与排除法的综合应用,考查分析与计算的能力,属于中档题.

练习册系列答案
相关题目
 ,求下列各式的值:
,求下列各式的值: ; (2)
; (2)  .
. ,
,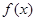 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程; 上的值域。
上的值域。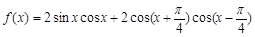 。
。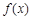 的单调递减区间; (2)设
的单调递减区间; (2)设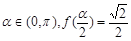 ,求
,求 的值。
的值。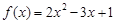 ,
, ,(
,(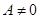 )
) ≤
≤ ≤
≤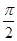 时,求
时,求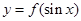 的最大值;
的最大值;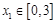 ,总存在
,总存在 ,使
,使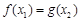 成立,求实数
成立,求实数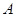 的取值范围;
的取值范围;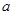 取何值时,方程
取何值时,方程 在
在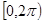 上有两解?
上有两解? (
( )的部分图像如右所示.
)的部分图像如右所示.
 的解析式;
的解析式; ,且
,且 ,求
,求 的值.
的值. 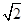 sin
sin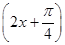 .
.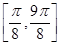 上的图象.
上的图象.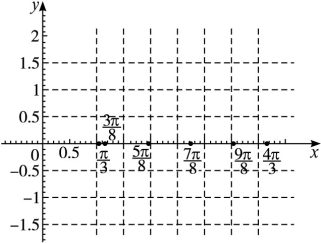

 .
.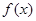 的定义域及最小正周期;
的定义域及最小正周期;
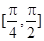 上的最值.
上的最值.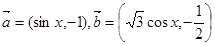 ,函数
,函数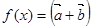 ·
·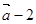
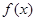 的最小正周期T及单调减区间
的最小正周期T及单调减区间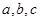 分别是△ABC内角A,B,C的对边,其中A为锐角,
分别是△ABC内角A,B,C的对边,其中A为锐角,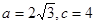 且
且 ,求A,b和△ABC的面积S
,求A,b和△ABC的面积S