题目内容
已知椭圆的中心为原点 ,长轴在
,长轴在 轴上,上顶点为
轴上,上顶点为 ,左、右焦点分别为
,左、右焦点分别为 ,线段
,线段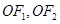 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过
是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;(Ⅱ)过 作直线交椭圆于
作直线交椭圆于 ,
, ,求△
,求△ 的面积
的面积

【答案】
:(Ⅰ) +
+ =1(Ⅱ)
=1(Ⅱ)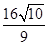
【解析】::(Ⅰ)如答(21)图,设所求椭圆的标准方程为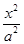 +
+ =1(
=1( ),右焦点为
),右焦点为 因
因 是直角三角形且
是直角三角形且 ,故
,故 为直角,从而
为直角,从而 ,即
,即 ,结合
,结合 得
得 。故
。故 ,
, 所以离心率
所以离心率 ,在
,在 中,
中, 故
故
由题设条件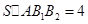 得
得 ,从而
,从而 因此所求 椭圆的的标准方程为:
因此所求 椭圆的的标准方程为: +
+ =1
=1
(Ⅱ)由(Ⅰ)知 ,由题意,直线
,由题意,直线 的倾斜角不为0,故可设直线
的倾斜角不为0,故可设直线 的方程为
的方程为 ,代入椭圆方程
,代入椭圆方程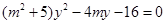 (*)
(*)
设 则
则 是上面方程的两根,因此
是上面方程的两根,因此
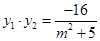 又
又 ,所以
,所以





 由
由 ,知
,知 ,即
,即 ,解得
,解得
当 时,方程(*)化为:
时,方程(*)化为:
故 ,
,
 的面积
的面积 当
当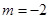 时,同理可得(或由对称性可得)
时,同理可得(或由对称性可得) 的面积
的面积 综上所述,
综上所述, 的面积为
的面积为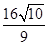

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 已知椭圆的中心为原点O,一个焦点为F
已知椭圆的中心为原点O,一个焦点为F ,长轴在
,长轴在 轴上,上顶点为
轴上,上顶点为 ,左、右焦点分别为
,左、右焦点分别为 ,线段
,线段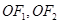 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程;
是面积为4的直角三角形。(Ⅰ)求该椭圆的离心率和标准方程; 作直线
作直线 交椭圆于
交椭圆于 ,
, ,求直线
,求直线