题目内容
已知甲同学每投篮一次,投进的概率均为
.
(1)求甲同学投篮4次,恰有3次投进的概率;
(2)甲同学玩一个投篮游戏,其规则如下:最多投篮6次,连续2次不中则游戏终止.设甲同学在一次游戏中投篮的次数为X,求X的分布列.
| 2 |
| 3 |
(1)求甲同学投篮4次,恰有3次投进的概率;
(2)甲同学玩一个投篮游戏,其规则如下:最多投篮6次,连续2次不中则游戏终止.设甲同学在一次游戏中投篮的次数为X,求X的分布列.
(1)设“甲投篮4次,恰有3次投进”为事件A,
则P(A)=
(
)3•(
)1=
.
(2)依题意,X的可能取值为2,3,4,5,6.
P(X=2)=
×
=
;
P(X=3)=
×
×
=
;
P(X=4)=(
+
)×
×
×
=
;
“X=5”表示投篮5次后终止投篮,即“最后两次投篮未进,第三次投中,第一次与第二次至少有一次投中”.
所以P(X=5)=[1-
•
]•
•(
)2=
;
P(X=6)=1-[P(X=2)+P(X=3)+P(X=4)+P(X=5)]=
.
所以,所求X的分布列为:
则P(A)=
| C | 34 |
| 2 |
| 3 |
| 1 |
| 3 |
| 32 |
| 81 |
(2)依题意,X的可能取值为2,3,4,5,6.
P(X=2)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
P(X=3)=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
P(X=4)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
“X=5”表示投篮5次后终止投篮,即“最后两次投篮未进,第三次投中,第一次与第二次至少有一次投中”.
所以P(X=5)=[1-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 16 |
| 243 |
P(X=6)=1-[P(X=2)+P(X=3)+P(X=4)+P(X=5)]=
| 164 |
| 243 |
所以,所求X的分布列为:
| X | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|

练习册系列答案
相关题目
 ,则
,则 ( )
( )



 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为 (
( ),已知他投篮一次得分的数学期望为2(不计其它得分情况),则
),已知他投篮一次得分的数学期望为2(不计其它得分情况),则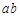 的最大值为( )
的最大值为( )



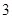 局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是
局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是 。假设各局比赛结果相互独立。
。假设各局比赛结果相互独立。 胜利的概率;
胜利的概率; 或
或 ,则胜利方得
,则胜利方得 分;若比赛结果为
分;若比赛结果为 ,则胜利方得
,则胜利方得 分、对方得
分、对方得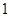 分。求乙队得分
分。求乙队得分 的分布列及数学期望。
的分布列及数学期望。 ,某班3名同学商定明天分别就同一问题询问服务中心,且每人只拨打一次,求他们中成功咨询的人数X的分布列.
,某班3名同学商定明天分别就同一问题询问服务中心,且每人只拨打一次,求他们中成功咨询的人数X的分布列.