题目内容
设z1=1-cosθ＋isinθ，z2=a2＋ai(a∈R).若z1·z2是纯虚数，问在(0，2π)内是否存在θ使(z1-z2)2是实数？
解：假设存在满足条件的θ，则由z1·z2为纯虚数可得
由上可知a≠0，cosθ≠1,∴a=
要使(z1-z2)2是实数，就是要(z1-z2)是实数或为纯虚数.
但是z1-z2=(1-cosθ-a2)＋(sinθ-a)i.
∴sinθ-a=0或1-cosθ-a2=0.
由
都可解得θ=
或θ=
.
故满足条件的θ存在.
练习册系列答案
相关题目
)2+
i,问在(0,2π)内是否存在θ,
|，θ是以x轴的非负半轴为始边、以OZ所在的射线为终边的角，复数z=a+bi还可以表示为z=r(cosθ+isinθ)，这个表达式叫做复数z的三角形式，其中，r叫做复数z的模，当r≠0时，θ叫做复数z的幅角，复数0的幅角是任意的，当0≤θ<2π时，θ叫做复数z的幅角主值，记作argz．
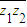=0，问在（0，2π）内是否存在θ使（z1-z2）2为实数？若存在，求出θ的值；若不存在，请说明理由．