题目内容
已知数列{an}的首项a1=
，
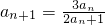，其中n∈N+．
（Ⅰ）求证：数列{
}为等比数列；
（Ⅱ）记Sn=
，若Sn＜100，求最大的正整数n．
（Ⅰ）证明：∵
，∴
，
∵
，∴
∈N+），
∴数列{}为等比数列．
（Ⅱ）解：由（Ⅰ）可求得
，∴
=
，
若Sn＜100，则n+1-
，
∴nmax=99．
分析：（Ⅰ）利用数列递推式，变形可得，从而可证数列{}为等比数列；
（Ⅱ）确定数列的通项，利用等比数列的求和公式求和，即可求最大的正整数n．
点评：本题考查数列递推式，考查等比数列的证明，考查等比数列的求和公式，属于中档题．
，∴，∵
，∴∈N+），∴数列{
}为等比数列．（Ⅱ）解：由（Ⅰ）可求得
，∴=，若Sn＜100，则n+1-
，∴nmax=99．
分析：（Ⅰ）利用数列递推式，变形可得
，从而可证数列{}为等比数列；（Ⅱ）确定数列的通项，利用等比数列的求和公式求和，即可求最大的正整数n．
点评：本题考查数列递推式，考查等比数列的证明，考查等比数列的求和公式，属于中档题．
练习册系列答案
相关题目