题目内容
设x、y为正实数,a= ,b=p
,b=p ,c=x+y.
,c=x+y.
(1)如果p=1,则是否存在以a、b、c为三边长的三角形?请说明理由;
(2)对 任意的正实数x、y,试探索当存在以a、b、c为三边长的三角形时p的取值范围.
任意的正实数x、y,试探索当存在以a、b、c为三边长的三角形时p的取值范围.
[解析] (1)存在以a、b、c为三边长的三角形.
当p=1时,b= .
.
∵c2=x2+y2+2xy>x2+y2+xy=a2,
∴c>a,又a2=x2+xy+y2>xy=b2,∴a>b,∴c>a>b,
 ∴a+b>c.
∴a+b>c.
即p=1时,存在以a、b、c为三边长的三角形.
 当且仅当t=1时,f(t)取最小值2+
当且仅当t=1时,f(t)取最小值2+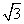 ,g(t)取最大值2-
,g(t)取最大值2-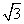 ,
,
因此p的取值范围为2-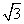 <p<2+
<p<2+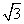 .
.
因此,当p的取值范围为2-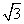 <p<2+
<p<2+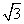 时,以a、b、c为三边的三角形总存在.
时,以a、b、c为三边的三角形总存在.

练习册系列答案
相关题目
 ,已知
,已知
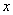 的不等式
的不等式 和
和 的解集分别为
的解集分别为 和
和 ,那么称这两个不等式为对偶不等式.如果不等式
,那么称这两个不等式为对偶不等式.如果不等式 与不等式
与不等式 为对偶不等式,且
为对偶不等式,且 ,那么
,那么 ______________.
______________. 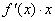 <
< 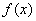 ,且f(2)=0,则
,且f(2)=0,则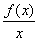 >0的解集为( )
>0的解集为( )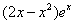 ,给出以下几个结论:
,给出以下几个结论: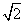 )是极小值,f(
)是极小值,f( 只有正根,则
只有正根,则 的取值范围是( )
的取值范围是( )  或
或 B
B 
 D
D 
 的解集为
的解集为  的定义域为开区间
的定义域为开区间 ,导函数
,导函数 在
在
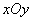 中,
中,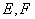 两点的坐标分别为
两点的坐标分别为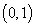 、
、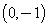 ,
, 满足:直线
满足:直线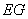 与直线
与直线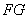 的斜率之积为
的斜率之积为 .
.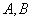 为动点
为动点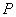 为直线
为直线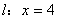 上的一动点(点
上的一动点(点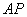 交
交 点,连
点,连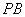 并延长交
并延长交 点,试问直线
点,试问直线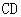 是否过定点?若
是否过定点?若