题目内容
如图，在区间[0，1]上给定曲线y=x2，试在此区间内确定点t的值，使图中阴影部分的面积S1+S2最小．
【答案】分析：先利用定积分分别表示出阴影部分的面积S1与S2，然后求出S1+S2关于t的函数解析式和定义域，利用导数研究函数的单调性，从而求出函数的最小值．
解答：解：
，
…（4分）
∴
…（6分）
令S′（t）=0，得
或t=0（舍去）
当
时，S′（t）＜0；当
时，S′（t）＞0；
∴当
时，S（t）为减函数，当
时，S（t）为增函数…（10分）
所以，当
时，
…（12分）
点评：本题主要考查了定积分在求面积中的应用，以及利用导数研究函数的单调性和求函数最值，属于中档题．
解答：解：
，…（4分）∴
…（6分）令S′（t）=0，得
或t=0（舍去）当
时，S′（t）＜0；当时，S′（t）＞0；∴当
时，S（t）为减函数，当时，S（t）为增函数…（10分）所以，当
时，…（12分）点评：本题主要考查了定积分在求面积中的应用，以及利用导数研究函数的单调性和求函数最值，属于中档题．
练习册系列答案
相关题目
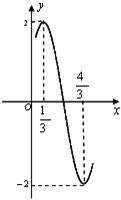已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0．|φ|＜
如图，在区间[0，1]上给定曲线y=x2，试在此区间内确定点t的值，使图中阴影部分的面积S1+S2最小．
