题目内容
已知F1,F2分别是椭圆 的左右焦点,已知点
的左右焦点,已知点 ,满足
,满足 ,设A、B是上半椭圆上满足
,设A、B是上半椭圆上满足 的两点,其中
的两点,其中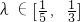 .
.
(1)求此椭圆的方程;
(2)求直线AB的斜率的取值范围.
解:(1)由于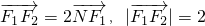 ,
,
∴ ,解得
,解得 ,
,
∴椭圆的方程是 .
.
(2)∵ ,∴A,B,N三点共线,
,∴A,B,N三点共线,
而N(-2,0),设直线的方程为y=k(x+2),(k≠0),
由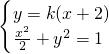 消去x得:
消去x得: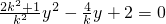
由 ,解得
,解得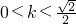 .
.
设A(x1,y1),B(x2,y2),由韦达定理得 ①,
①,
又由 得:(x1+2,y1)=λ(x2+2,y2),∴y1=λy2②.
得:(x1+2,y1)=λ(x2+2,y2),∴y1=λy2②.
将②式代入①式得: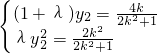 ,
,
消去y2得: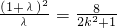 .
.
设 ,当
,当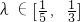 时,?(λ)是减函数,
时,?(λ)是减函数,
∴ ,∴
,∴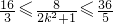 ,
,
解得 ,又由
,又由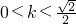 得
得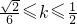 ,
,
∴直线AB的斜率的取值范围是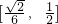 .
.
分析:(1)有题意及椭圆的方程和性质利用 ,可以列出 a,b,c的方程,解出即可;
,可以列出 a,b,c的方程,解出即可;
(2)由题意先设直线的方程为y=k(x+2)(k≠0),把直线方程与椭圆方程进行联立,利用韦达定理整体代换,借助于与 ,得到k,λ的关系式,用λ表示k,有λ的范围再求出k的范围.
,得到k,λ的关系式,用λ表示k,有λ的范围再求出k的范围.
点评:此题考查了椭圆的方程及椭圆的基本性质,直线方程与椭圆方程进行联立设而不求及整体代换的思想,还考查了利用均值不等式求值域.
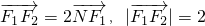 ,
,∴
 ,解得
,解得 ,
,∴椭圆的方程是
 .
.(2)∵
 ,∴A,B,N三点共线,
,∴A,B,N三点共线,而N(-2,0),设直线的方程为y=k(x+2),(k≠0),
由
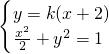 消去x得:
消去x得: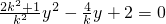
由
 ,解得
,解得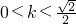 .
.设A(x1,y1),B(x2,y2),由韦达定理得
 ①,
①,又由
 得:(x1+2,y1)=λ(x2+2,y2),∴y1=λy2②.
得:(x1+2,y1)=λ(x2+2,y2),∴y1=λy2②.将②式代入①式得:
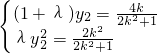 ,
,消去y2得:
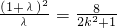 .
.设
 ,当
,当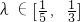 时,?(λ)是减函数,
时,?(λ)是减函数,∴
 ,∴
,∴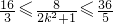 ,
,解得
 ,又由
,又由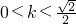 得
得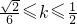 ,
,∴直线AB的斜率的取值范围是
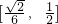 .
.分析:(1)有题意及椭圆的方程和性质利用
 ,可以列出 a,b,c的方程,解出即可;
,可以列出 a,b,c的方程,解出即可;(2)由题意先设直线的方程为y=k(x+2)(k≠0),把直线方程与椭圆方程进行联立,利用韦达定理整体代换,借助于与
 ,得到k,λ的关系式,用λ表示k,有λ的范围再求出k的范围.
,得到k,λ的关系式,用λ表示k,有λ的范围再求出k的范围.点评:此题考查了椭圆的方程及椭圆的基本性质,直线方程与椭圆方程进行联立设而不求及整体代换的思想,还考查了利用均值不等式求值域.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: