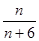题目内容
数列![]() 的各项均为正数,
的各项均为正数,![]() 为其前
为其前![]() 项和,对于任意
项和,对于任意![]() ,总有
,总有![]() 成等差数列.
成等差数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若b![]() =a
=a![]() 4
4![]() (
(![]() ), B
), B![]() 是数列{b
是数列{b![]() }的前
}的前![]() 项和,求证:不等式 B
项和,求证:不等式 B![]() ≤4B
≤4B![]() ,对任意
,对任意![]() 皆成立.
皆成立.
(3)令![]()
解:(1)由已知:对于![]() ,总有
,总有![]() ①成立
①成立
∴![]() (n ≥ 2)②
(n ≥ 2)②
①―②得![]() , ∴
, ∴![]()
∵![]() 均为正数,∴
均为正数,∴![]() (n ≥ 2)
(n ≥ 2)
∴数列![]() 是公差为1的等差数列
是公差为1的等差数列
又n=1时,![]() ,
,
解得![]() =1 ∴
=1 ∴![]() .(
.(![]() )
)
(2)b![]() = n+4
= n+4![]() , 所以数列{b
, 所以数列{b![]() }的前
}的前![]() 项和
项和![]()
∴对任意的![]() ,
,![]()
![]() .
.
所以不等式![]() ,对任意
,对任意![]() 皆成立.
皆成立.
(3)由(1)知![]()
![]()
![]()

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目






 的前n项和为
的前n项和为 ,则下列命题:
,则下列命题: 也是递增数列;
也是递增数列; ),则
),则 的充要条件是
的充要条件是
 的充要条件是
的充要条件是
 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 ,总有
,总有 成等差数列。设数列
成等差数列。设数列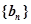 的前
的前 ,且
,且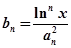 ,则对任意实数
,则对任意实数 (
( 是常数,
是常数, )和任意正整数
)和任意正整数 的各项均为正数,
的各项均为正数, 为其前n项和,对于任意的
为其前n项和,对于任意的 ,总有
,总有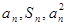 成等差数列,又记
成等差数列,又记 ,数列
,数列 的前n项和Tn=( )
的前n项和Tn=( ) B.
B.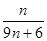 C.
C. D.
D.