题目内容
A、B、C为△ABC的三内角，且其对边分别为a、b、c， 若
,
，且
·
＝
（1）求角A的大小；
（2）若a＝2
，三角形面积S＝，求b+c的值
解析:（1）∵，，且·＝，
∴－cos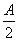2
＋sin2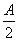＝， 即－cosA＝，又A∈(0，)，
∴A＝
（2）S△ABC＝bc·sinA＝b·c·sin＝，∴bc＝4,
又由余弦定理得：a2=b2+c2－2bc·cos120°＝b2+c2+bc ,
∴16＝(b+c)2，故b+c＝4
练习册系列答案
相关题目
，正实数
满足
且
。若实数
是方程
的一个解，那么下列四个判断：①
②
③
④
中有可能成立的个数为（ ）
的最小值为( )
C. 4 D. 
，点C在
的边AC上， 
，则
等于( ) 
B. 3 C. 
D. 
中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D。
；
的值。
，0) B．(0，
) D．(
)
，其中i是虚数单位，则|z|＝ ．
的各项均为正数，它的前
项的和为
，点
在函数
的图像上；数列
满足
．其中
．
，求证：数列
的前
（