题目内容
在数列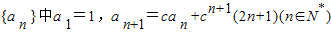 ,其中c≠0.
,其中c≠0.(Ⅰ)求
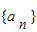 通项公式;
通项公式;(Ⅱ)若对一切k∈N*有
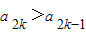 ,求c的取值范围.
,求c的取值范围.
【答案】分析:(1)由数列 ,其中c≠0.求得a1=1,a2=ca1+c2•3=3c2+c,a3=ca2+c3•5=8c3+c2,由此猜测an=(n2-1)cn+cn-1,进而用数学归纳法证明.
,其中c≠0.求得a1=1,a2=ca1+c2•3=3c2+c,a3=ca2+c3•5=8c3+c2,由此猜测an=(n2-1)cn+cn-1,进而用数学归纳法证明.
(2)把(1)中求得的an代入 ,整理得(4k2-1)c2-(4k2-4k-1)c-1>0,设(4k2-1)c2-(4k2-4k-1)c-1=0的两个根分别表示ck和c
,整理得(4k2-1)c2-(4k2-4k-1)c-1>0,设(4k2-1)c2-(4k2-4k-1)c-1=0的两个根分别表示ck和c ,根据ck<
,根据ck< =
= ,得c≥1;再根据
,得c≥1;再根据 判断出单调递增知
判断出单调递增知 ≥
≥ 对一切k∈N*成立,求得c<-
对一切k∈N*成立,求得c<- .最后综合答案可得.
.最后综合答案可得.
解答:解:(1)∵数列 ,其中c≠0.
,其中c≠0.
∴a1=1,
a2=ca1+c2•3=(22-1)c2+c,
a3=ca2+c3•5=(32-1)c3+c2,
由此猜测an=(n2-1)cn+cn-1,
下用数学归纳法证明.
①当n=1时,等式成立;
②假设当n=k时,等式成立,即ak=(k2-1)ck+ck-1,…(6分)
则当n=k+1时,ak+1=cak+ck+1(2k+1)=c[(k2-1)ck+ck-1]+ck+1(2k+1)
=(k2+2k)ck+1+ck=[(k+1)2-1]ck+1+ck,…(7分)
综上,an=(n2-1)cn+cn-1对任何n∈N*都成立.…(8分)
(3)由a2k>a2k-1,得[(2k)2-1]c2k+c2k-1>[(2k-1)2-1]c2k-1+c2k-2,…(9分)
因c2k-2>0,所以(4k2-1)c2-(4k2-4k-1)c-1>0.
解此不等式得:对一切k∈N*,有c>ck或c<c ,
,
其中ck= ,
,
 =
= .(10分)
.(10分)
∴ ,
,
又由 <
< =4k2+1,
=4k2+1,
知ck< =
= ,…(11分)
,…(11分)
因此由c>ck对一切k∈N*成立得c≥1.…(12分)
∵ =
= <0,
<0,
∴ 单调递增,故
单调递增,故 ≥
≥ 对一切k∈N*成立,
对一切k∈N*成立,
因此由c< 对一切k∈N*成立得c<
对一切k∈N*成立得c< =-
=- .…(13分)
.…(13分)
从而c的取值范围为(-∞,- )∪[1,+∞).…(14分).
)∪[1,+∞).…(14分).
点评:本题主要考查了数列的递推式、数学归纳法,考查了学生综合运用所学知识和实际的运算能力.考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
 ,其中c≠0.求得a1=1,a2=ca1+c2•3=3c2+c,a3=ca2+c3•5=8c3+c2,由此猜测an=(n2-1)cn+cn-1,进而用数学归纳法证明.
,其中c≠0.求得a1=1,a2=ca1+c2•3=3c2+c,a3=ca2+c3•5=8c3+c2,由此猜测an=(n2-1)cn+cn-1,进而用数学归纳法证明.(2)把(1)中求得的an代入
 ,整理得(4k2-1)c2-(4k2-4k-1)c-1>0,设(4k2-1)c2-(4k2-4k-1)c-1=0的两个根分别表示ck和c
,整理得(4k2-1)c2-(4k2-4k-1)c-1>0,设(4k2-1)c2-(4k2-4k-1)c-1=0的两个根分别表示ck和c ,根据ck<
,根据ck< =
= ,得c≥1;再根据
,得c≥1;再根据 判断出单调递增知
判断出单调递增知 ≥
≥ 对一切k∈N*成立,求得c<-
对一切k∈N*成立,求得c<- .最后综合答案可得.
.最后综合答案可得.解答:解:(1)∵数列
 ,其中c≠0.
,其中c≠0.∴a1=1,
a2=ca1+c2•3=(22-1)c2+c,
a3=ca2+c3•5=(32-1)c3+c2,
由此猜测an=(n2-1)cn+cn-1,
下用数学归纳法证明.
①当n=1时,等式成立;
②假设当n=k时,等式成立,即ak=(k2-1)ck+ck-1,…(6分)
则当n=k+1时,ak+1=cak+ck+1(2k+1)=c[(k2-1)ck+ck-1]+ck+1(2k+1)
=(k2+2k)ck+1+ck=[(k+1)2-1]ck+1+ck,…(7分)
综上,an=(n2-1)cn+cn-1对任何n∈N*都成立.…(8分)
(3)由a2k>a2k-1,得[(2k)2-1]c2k+c2k-1>[(2k-1)2-1]c2k-1+c2k-2,…(9分)
因c2k-2>0,所以(4k2-1)c2-(4k2-4k-1)c-1>0.
解此不等式得:对一切k∈N*,有c>ck或c<c
 ,
,其中ck=
 ,
, =
= .(10分)
.(10分)∴
 ,
,又由
 <
< =4k2+1,
=4k2+1,知ck<
 =
= ,…(11分)
,…(11分)因此由c>ck对一切k∈N*成立得c≥1.…(12分)
∵
 =
= <0,
<0,∴
 单调递增,故
单调递增,故 ≥
≥ 对一切k∈N*成立,
对一切k∈N*成立,因此由c<
 对一切k∈N*成立得c<
对一切k∈N*成立得c< =-
=- .…(13分)
.…(13分)从而c的取值范围为(-∞,-
 )∪[1,+∞).…(14分).
)∪[1,+∞).…(14分).点评:本题主要考查了数列的递推式、数学归纳法,考查了学生综合运用所学知识和实际的运算能力.考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
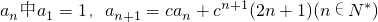 ,其中c≠0.
,其中c≠0. 通项公式;
通项公式;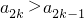 ,求c的取值范围.
,求c的取值范围.