题目内容
设 ![]() . 记
. 记![]() ,
,![]()
![]() ,
,
![]() . 证明:
. 证明:![]()
【证明】(1)如果![]() ,则
,则![]() ,
,![]() 。
。
(2)如果![]() ,由题意
,由题意 ![]() ,
,![]() ,
,![]() . 则
. 则
① 当 ![]() 时,
时,![]() (
(![]() ).
).
事实上,当![]() 时,
时,![]() , 设
, 设![]() 时成立(
时成立(![]() 为某整数),则对
为某整数),则对![]() ,
,
![]() .
.
② 当 ![]() 时,
时,![]() (
(![]() ).
).
事实上,当![]() 时,
时,![]() , 设
, 设![]() 时成立(
时成立(![]() 为某整数),则对
为某整数),则对![]() ,有
,有
![]() .注意到 当
.注意到 当![]() 时,总有
时,总有![]() ,即
,即 ![]() . 从而有
. 从而有![]() .由归纳法,推出
.由归纳法,推出 ![]() 。
。
(3)当![]() 时,记
时,记![]() ,则对于任意
,则对于任意![]() ,
,![]() 且
且
![]() 。
。
对于任意![]() ,
,![]() , 则
, 则![]() 。
。
所以,![]() 。当
。当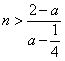 时,
时,![]() ,即
,即![]() 。因此
。因此![]() 。
。

练习册系列答案
相关题目
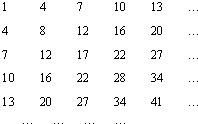 下述数阵称为“森德拉姆筛”,记为S.其特点是每行每列都是等差数列,第i行第j列的数记为Aij.
下述数阵称为“森德拉姆筛”,记为S.其特点是每行每列都是等差数列,第i行第j列的数记为Aij.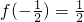 ,记an=f(2n),n∈N*,求数列{an}的前n项和Sn;
,记an=f(2n),n∈N*,求数列{an}的前n项和Sn;