题目内容
已知半椭圆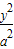 +
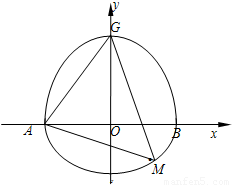
+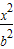 =1(y≥0,a>b>0)和半圆x2+y2=b2(y≤0)组成的曲线C如图所示.曲线C交x轴于点A,B,交y轴于点G,H,点M是半圆上异于A,B的任意一点,当点M位于点(
=1(y≥0,a>b>0)和半圆x2+y2=b2(y≤0)组成的曲线C如图所示.曲线C交x轴于点A,B,交y轴于点G,H,点M是半圆上异于A,B的任意一点,当点M位于点(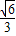 ,-
,-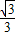 )时,△AGM的面积最大,则半椭圆的方程为 .
)时,△AGM的面积最大,则半椭圆的方程为 .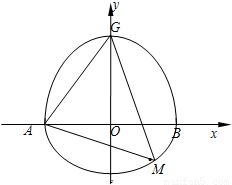
【答案】分析:由点M(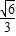 ,-
,-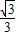 )在半圆上,可求b,然后求出G,H,A,根据已知AGM的面积最大的条件可知,OM⊥AG,
)在半圆上,可求b,然后求出G,H,A,根据已知AGM的面积最大的条件可知,OM⊥AG,
即KOM•KAG=-1,代入可求a,进而可求椭圆方程
解答:解:由点M(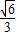 ,-
,-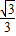 )在半圆上,
)在半圆上,
所以b=1,
∵G(0,a),H(0,-a),A(-b,0)
而当点M位于(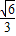 ,-
,-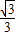 )时,△AGM的面积最大可知,OM⊥AG,
)时,△AGM的面积最大可知,OM⊥AG,
即KOM•KAG=-1,
∵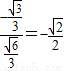 ,KAG=
,KAG=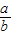 =a
=a
∴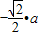 ═-1
═-1
∴a=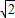 ,b=1
,b=1
所以半椭圆的方程为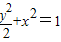 (y≥0)
(y≥0)
故答案为: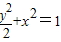 (y≥0)
(y≥0)
点评:本题主要考查了椭圆方程的求解,直线的垂直与斜率关系的应用,解题的关键是灵活利用椭圆的性质
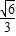 ,-
,-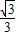 )在半圆上,可求b,然后求出G,H,A,根据已知AGM的面积最大的条件可知,OM⊥AG,
)在半圆上,可求b,然后求出G,H,A,根据已知AGM的面积最大的条件可知,OM⊥AG,即KOM•KAG=-1,代入可求a,进而可求椭圆方程
解答:解:由点M(
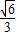 ,-
,-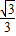 )在半圆上,
)在半圆上,所以b=1,
∵G(0,a),H(0,-a),A(-b,0)
而当点M位于(
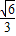 ,-
,-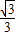 )时,△AGM的面积最大可知,OM⊥AG,
)时,△AGM的面积最大可知,OM⊥AG,即KOM•KAG=-1,
∵
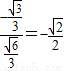 ,KAG=
,KAG=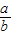 =a
=a∴
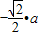 ═-1
═-1∴a=
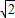 ,b=1
,b=1所以半椭圆的方程为
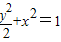 (y≥0)
(y≥0)故答案为:
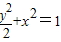 (y≥0)
(y≥0)点评:本题主要考查了椭圆方程的求解,直线的垂直与斜率关系的应用,解题的关键是灵活利用椭圆的性质

练习册系列答案
相关题目
 已知半椭圆
已知半椭圆 已知半椭圆
已知半椭圆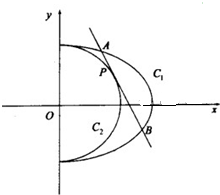 (2013•济宁一模)如图,已知半椭圆C1:
(2013•济宁一模)如图,已知半椭圆C1: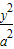 +
+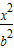 =1(y≥0,a>b>0)和半圆x2+y2=b2(y≤0)组成的曲线C如图所示.曲线C交x轴于点A,B,交y轴于点G,H,点M是半圆上异于A,B的任意一点,当点M位于点(
=1(y≥0,a>b>0)和半圆x2+y2=b2(y≤0)组成的曲线C如图所示.曲线C交x轴于点A,B,交y轴于点G,H,点M是半圆上异于A,B的任意一点,当点M位于点(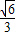 ,-
,-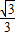 )时,△AGM的面积最大,则半椭圆的方程为 .
)时,△AGM的面积最大,则半椭圆的方程为 .