Question

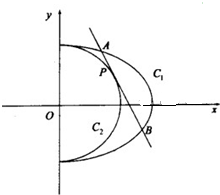（2013•济宁一模）如图，已知半椭圆C₁：

x2

a2

+y²=1（a＞1，x≥0）的离心率为

2

2

，曲线C₂是以半椭圆C₁的短轴为直径的圆在y轴右侧的部分，点P（x₀，y₀）是曲线C₂上的任意一点，过点P且与曲线C₂相切的直线l与半椭圆C₁交于不同点A，B．
（I）求a的值及直线l的方程（用x₀，y₀表示）；
（Ⅱ）△OAB的面积是否存在最大值？若存在，求出最大值；若不存在，请说明理由．

Answer 1

分析：（I）利用离心率计算公式e=

c

a

=

1- b2 a2

及已知即可得出a．设Q（x，y）为直线l上任意一点，利用圆的切线的性质可得

OP

⊥

PQ

，即

OP

•

PQ

=0．进而即可求出．
（II）分切点P为（1，0）和不为（1，0）时两种情况讨论．把切线l的方程与椭圆方程联立得到根与系数的关系，利用弦长公式、基本不等式的性质、三角形的面积计算公式即可得出．

解答：解：（I）∵半椭圆C₁的离心率为

2

2

，∴e=

c

a

=

1- a2-1 a2

=

2

2

，
∴a=

2

．
设Q（x，y）为直线l上任意一点，则

OP

⊥

PQ

，即

OP

•

PQ

=0．
∴（x₀，y₀）•（x-x₀，y-y₀）=0，化为x0x+y0y=

x

2 0

+

y

2 0

．
又∵

x

2 0

+

y

2 0

=1，∴直线l的方程为x₀x+y₀y-1=0．
（II）①当P点不为（1，0）时，

x0x+y0y-1=0 x2+2y2=2

，
得(2

x

2 0

+

y

2 0

)x2-4x0x+2-2

y

2 0

=0，即(

x

2 0

+1)x2-4x0x+2

x

2 0

=0．
设A（x₁，y₁），B（x₂，y₂），∴

x1+x2= 4x0 x 2 0 +1 x1x2= 2 x 2 0 x 2 0 +1

∵|AB|=

1+k2

•

(x1+x2)2-4x1x2

=

8 x 2 0 (1- x 2 0 ) (1- x 2 0 )( x 2 0 +1)2

=

8 x 2 0 x 4 0 +2 x 2 0 +1

=

8 x 2 0 + 1 x 2 0 +2

＜

8 2 x 2 0 • 1 x 2 0 +2

=

2

∴S_△OAB=|AB||OP|=

1

2

|AB|＜

2

2

．
②当P点为（1，0）时，此时，S△OAB=

2

2

．
综上，由①②可得，△OAB面积的最大值为

2

2

．

点评：本题考查了椭圆及圆的标准方程及其性质、直线与椭圆相交问题、根与系数的关系、基本不等式的性质、三角形的面积向量垂直于数量积得关系等基础知识与基本技能，考查了推理能力和计算能力．