Question

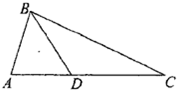如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=

3

BD，BC=2BD，则sinC的值为

6

6

．

Answer 1

分析：在△ABD中，利用余弦定理可得cos∠ADB=

a2+ 4a2 3 -a2

2a× 2a 3

=

3

3

，从而sin∠ADB=

6

3

，即sin∠BDC=

6

3

在△BDC中，利用正弦定理，可求sinC的值

解答：解：设AB=a，则
∵AB=AD，2AB=

3

BD，BC=2BD
∴AD=a，BD=

2a

3

，BC=

4a

3

在△ABD中，cos∠ADB=

a2+ 4a2 3 -a2

2a× 2a 3

=

3

3

∴sin∠ADB=

6

3

∴sin∠BDC=

6

3

在△BDC中，

BD

sin∠C

=

BC

sin∠BDC

∴sin∠C=

BD×sin∠BDC

BC

=

6

6

故答案为：

6

6

点评：本题重点考查余弦定理、正弦定理的运用，解题的关键是确定余弦定理、正弦定理运用的三角形，属于基础题．