题目内容
(本小题12分)已知c>0,设p:函数 在R上单调递减;q:不等式
在R上单调递减;q:不等式
 >1的解集为R,如果“p或q”为真,且“p且q”为假,求c的取值范围。
>1的解集为R,如果“p或q”为真,且“p且q”为假,求c的取值范围。
【答案】
1)由AB=2,AD= ,∠BAD=30,及余弦定理得
,∠BAD=30,及余弦定理得
 BD2=AB2+AD2-2AB·ADcos∠BAD=1,
BD2=AB2+AD2-2AB·ADcos∠BAD=1,
∵AD2+BD2=AB2,∴AD⊥BD.
∵SD⊥平面ABCD,AD 平面ABCD,
平面ABCD,
∴AD⊥SD,
∴AD⊥平面SBD,又SB 平面SBD,
平面SBD,
∴AD⊥SB.
(2)取CD的中点G,连结EG,则EG⊥面BCD,且EG=1.
连AC交BD于F,连FG,则FG//BC且FG= ,又BC⊥BD,∴FG⊥BD
,又BC⊥BD,∴FG⊥BD
∴ 即为所求二面角的平面角
即为所求二面角的平面角
在Rt 中,
中,
∴ 。
。
【解析】略

练习册系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线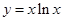
 处的切线方程。
处的切线方程。