Question

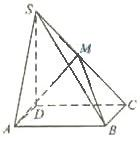如图，四棱锥S-ABCD中，底面ABCD为矩形，SD⊥底面ABCD，AD=

2

，DC=SD=2，点M在侧棱SC上，∠ABM=60°
（I）证明：M是侧棱SC的中点；
（2）求二面角S-AM-B的大小．

Answer 1

分析：（1）法一：要证明M是侧棱SC的中点，作MN∥SD交CD于N，作NE⊥AB交AB于E，连ME、NB，则MN⊥面ABCD，ME⊥AB，NE=AD=

2

设MN=x，则NC=EB=x，解RT△MNE即可得x的值，进而得到M为侧棱SC的中点；
法二：分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D-xyz，并求出S点的坐标、C点的坐标和M点的坐标，然后根据中点公式进行判断；
法三：分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D-xyz，构造空间向量，然后数乘向量的方法来证明．
（2）我们可以以D为坐标原点，分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D-xyz，我们可以利用向量法求二面角S-AM-B的大小．

解答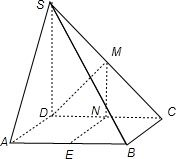：证明：（Ⅰ）作MN∥SD交CD于N，作NE⊥AB交AB于E，
连ME、NB，则MN⊥面ABCD，ME⊥AB，NE=AD=

2

设MN=x，则NC=EB=x，
在RT△MEB中，∵∠MBE=60°∴ME=

3

x．
在RT△MNE中由ME²=NE²+MN²∴3x²=x²+2
解得x=1，从而MN=

1

2

SD∴M为侧棱SC的中点M．
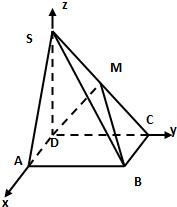
（Ⅰ）证法二：分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D-xyz，则A(

2

，0，0)，B(

2

，2，0)，C(0，0，2)，S(0，0，2)．
设M（0，a，b）（a＞0，b＞0），
则

BA

=(0，-2，0)，

BM

=(-

2

，a-2，b)，

SM

=(0，a，b-2)，

SC

=(0，2，-2)，
由题得

cos＜ BA BM ＞= 1 2 SM ∥ SC

，
即

-2(a-2) 2• (a-2)2+b2+2 = 1 2 -2a=2(b-2)

解之个方程组得a=1，b=1即M（0，1，1）
所以M是侧棱SC的中点．

（I）证法三：设

SM

=λ

MC

，
则M(0，

2λ

1+λ

，

2

1+λ

)，

MB

=(

2

，

2

1+λ

，

-2

1+λ

)
又

AB

=(0，2，0)，＜

MB

，

AB

＞=60o
故

MB

•

AB

=|

MB

|•|

AB

|cos60o，
即

4

1+λ

=

2+( 2 1+λ )2+( 2 1+λ )2

，
解得λ=1，所以M是侧棱SC的中点．
（Ⅱ）由（Ⅰ）得M(0，1，1)，

MA

=(

2

，-1，-1)，
又

AS

=(-

2

，0，2)，

AB

=(0，2，0)，
设

n1

=(x1，y1，z1)，

n2

=(x2，y2，z2)分别是平面SAM、MAB的法向量，
则

n1 • MA =0 n1 • AS =0

且

n2 • MA =0 n2 • AB =0

，
即

2 x1-y1-z1=0 - 2 x1+2z1=0

且

2 x2-y2-z2=0 2y2=0

分别令x1=x2=

2

得z₁=1，y₁=1，y₂=0，z₂=2，
即

n1

=(

2

，1，1)，

n2

=(

2

，0，2)，
∴cos＜

n1

，

n2

＞=

2+0+2

2• 6

=

6

3

二面角S-AM-B的大小π-arccos

6

3

．

点评：空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值；
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值；
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值；