Question

【题目】已知函数.

（1）求函数的极值；

（2）若， 是方程（）的两个不同的实数根，求证： .

Answer 1

【答案】（1）有极小值，无极大值.（2）见解析

【解析】试题分析：

（1）求出导函数，再求出的零点，确定零点两侧的正负，得极值；

（2）关键是参数的转换，由是某方程的解，代入得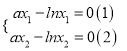，两式相减可解得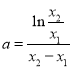，这样要证的不等式即为证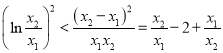，这样可用换元法，设，且不妨役，于是有，只要证，此时又可转化为求函数的最大值，求出的导数， ，为确定的正负及零点，可对函数求导，利用导数确定它的单调性，最终确定的单调性，从而得出结论．

试题解析：

（1）依题意，

故当时， ，当时，

故当时，函数有极小值，无极大值.

（2）因为， 是方程的两个不同的实数根.

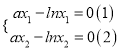∴两式相减得，解得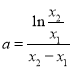

要证： ，即证： ，即证： ，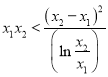

即证，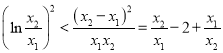

不妨设，令.只需证.

设，∴；

令，∴，∴在上单调递减，

∴ ，∴，∴在为减函数，∴.

即在恒成立，∴原不等式成立，即.