题目内容
已知△ABC是腰长为2的等腰直角三角形，点P是斜边BC上任意一点，则
•（
+
）的值是（ ）
| AB |
| AP |
| AC |
分析：由题意可得
•
=0，故
•（
+
）=
•
=
•
+
2=2×|
|cos135°+4，由此得出结论．
| AB |
| AC |
| AB |
| AP |
| AC |
| AB |
| AP |
| AB |
| BP |
| AB |
| BP |
解答：解：由题意可得
•
=0，故
•（
+
）=
•
+
•
=
•
=
•(
-
)=
•
+
2=2×|
|cos135°+4，
此值显然与|
|的值有关，即与点P在BC上的位置有关，
故选D．
| AB |
| AC |
| AB |
| AP |
| AC |
| AB |
| AP |
| AB |
| AC |
=
| AB |
| AP |
| AB |
| BP |
| BA |
| AB |
| BP |
| AB |
| BP |
此值显然与|
| BP |
故选D．
点评：本题主要考查两个向量的数量积的定义，两个向量垂直的性质，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
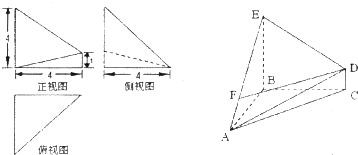
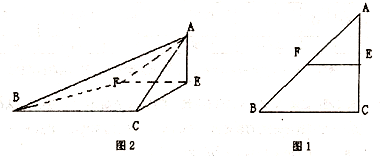已知△ABC是腰长为2的等腰直角三角形（如图1），∠BCA=90°，在边AC、AB上分别取点E、F、，使得EF∥BC，把△AEF沿直线EF折起，使∠AEC=90°，得四棱锥A-ECBF（如图2）．在四棱锥A-ECBF中，
•（
+
）的值是