题目内容
已知向量a=(3cosα,1),b=(-2,3sinα),且a⊥b,其中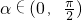 .
.
(1)求sinα和cosα的值;
(2)若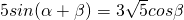 ,β∈(0,π),求角β的值.
,β∈(0,π),求角β的值.
解:(1)∵ ,∴
,∴ ,即sinα=2cosα,
,即sinα=2cosα,
又∵sin2α+cos2α=1,∴ ,
, ,∴
,∴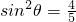 ,
,
又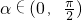 ,∴
,∴ .
.
(2)∵ ,
,
∴cosβ=sinβ,即tanβ=1,
∵β∈(0,π),∴
:答sinα和cosα的值为 ;角β的值为
;角β的值为
分析:(1)用向量垂直的充要条件的sinα=2cosα;再用三角函数的平方关系求值.
(2)用三角函数的和角公式展开求得tanβ=-1,进一步求出β.
点评:本题考查向量垂直的充要条件和三角函数的和角公式.
 ,∴
,∴ ,即sinα=2cosα,
,即sinα=2cosα,又∵sin2α+cos2α=1,∴
 ,
, ,∴
,∴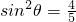 ,
,又
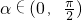 ,∴
,∴ .
.(2)∵
 ,
,∴cosβ=sinβ,即tanβ=1,
∵β∈(0,π),∴

:答sinα和cosα的值为
 ;角β的值为
;角β的值为
分析:(1)用向量垂直的充要条件的sinα=2cosα;再用三角函数的平方关系求值.
(2)用三角函数的和角公式展开求得tanβ=-1,进一步求出β.
点评:本题考查向量垂直的充要条件和三角函数的和角公式.

练习册系列答案
相关题目