题目内容
已知函数
 ,且
,且 的最大值为2,其图象相邻两对称轴间的距离为2,并过点
的最大值为2,其图象相邻两对称轴间的距离为2,并过点 .
.
(1)求 的值;
的值;
(2)若函数 在
在 上的图象与
上的图象与 轴的交点分别为
轴的交点分别为 、
、 ,求
,求 与
与 的夹角.
的夹角.

 ,且
,且 的最大值为2,其图象相邻两对称轴间的距离为2,并过点
的最大值为2,其图象相邻两对称轴间的距离为2,并过点 .
.(1)求
 的值;
的值;(2)若函数
 在
在 上的图象与
上的图象与 轴的交点分别为
轴的交点分别为 、
、 ,求
,求 与
与 的夹角.
的夹角.(1) . (2)即
. (2)即 与
与 的夹角为
的夹角为 .
.
 . (2)即
. (2)即 与
与 的夹角为
的夹角为 .
. 本试题主要是考查了三角函数图像的性质以及三角函数解析式的求解,以及运用图像与图像的交点问题,解决点的坐标,进而求解向量的数量积问题的综合运用。
(1)根据三角函数中相邻对称轴之间的距离即为半个周期求解得到w的值,以及最值得到A的值,然后代点得到参数 的值。
的值。
(2)根据第一问,利用三角函数与x轴的交点得到M,N的坐标,然后表示向量的数量积,得到夹角公式。
(1)由题可知, ,即
,即 ;
;  ,即
,即 ,
, ,
, .
.
∴ , 又其图象过点
, 又其图象过点 ,
,
∴ ,即
,即 ,
, ,
,
∴ (
( ),而
),而 ,故
,故  . …… 6分
. …… 6分
(2)由(1)可知, ,
,
∴ 由函数 的图象易知,
的图象易知, ,
, , 又
, 又 ,故
,故 ,
, . ∴
. ∴  ,即
,即 与
与 的夹角为
的夹角为
(1)根据三角函数中相邻对称轴之间的距离即为半个周期求解得到w的值,以及最值得到A的值,然后代点得到参数
 的值。
的值。(2)根据第一问,利用三角函数与x轴的交点得到M,N的坐标,然后表示向量的数量积,得到夹角公式。
(1)由题可知,
 ,即
,即 ;
;  ,即
,即 ,
, ,
, .
.∴
 , 又其图象过点
, 又其图象过点 ,
,∴
 ,即
,即 ,
, ,
,∴
 (
( ),而
),而 ,故
,故  . …… 6分
. …… 6分(2)由(1)可知,
 ,
,∴ 由函数
 的图象易知,
的图象易知, ,
, , 又
, 又 ,故
,故 ,
, . ∴
. ∴  ,即
,即 与
与 的夹角为
的夹角为

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,其图象与直线
,其图象与直线 的某两个交点横坐标为
的某两个交点横坐标为 ,
, 的最小值为
的最小值为 ,则
,则  ,
,
 ,
,
 ,
, x―
x― )的一个周期的图象(要求具有数量特征),并且写出由函数y=sinx变化到函数y=2sin(
)的一个周期的图象(要求具有数量特征),并且写出由函数y=sinx变化到函数y=2sin(






 中,
中, 的对边分别为
的对边分别为 且
且 成等差数列.
成等差数列. 的范围.
的范围. (
( )的最小正周
)的最小正周 ,
, 的值;
的值; 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数
 上的最小值.
上的最小值.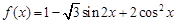 .
.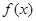 的最大值及取得最大值时的
的最大值及取得最大值时的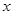 集合;
集合;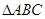 的角
的角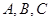 的对边分别为
的对边分别为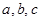 ,且
,且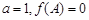 .求
.求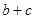 的取值范围
的取值范围 的单调递增区间的是
的单调递增区间的是




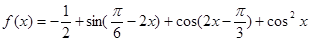
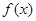 的最小正周期;
的最小正周期;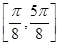 上的最大值,并求出
上的最大值,并求出 化简
化简
 均为锐角,
均为锐角, ,求
,求 的值
的值