题目内容
(本小题满分12分)
在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是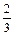 ,每次命中与否互相独立.
,每次命中与否互相独立.
(1) 求油罐被引爆的概率.
(2) 如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望。
在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是
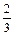 ,每次命中与否互相独立.
,每次命中与否互相独立.(1) 求油罐被引爆的概率.
(2) 如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望。
(1)油罐被引爆的概率为
(2)Eξ=2× +3×
+3× +4×
+4× +5×
+5× =
=

(2)Eξ=2×
 +3×
+3× +4×
+4× +5×
+5× =
=
解:(1)“油罐被引爆”的事件为事件A,其对立事件为 ,则P(
,则P( )=C
)=C …4分
…4分
∴P(A)=1-
答:油罐被引爆的概率为 …………6分
…………6分
(2)射击次数ξ的可能取值为2,3,4,5,…………7分
P(ξ=2)= , P(ξ=3)=C
, P(ξ=3)=C ,
,
P(ξ=4)=C , P(ξ=5)=C
, P(ξ=5)=C …………10分
…………10分
故ξ的分布列为:
Eξ=2× +3×
+3× +4×
+4× +5×
+5× =
= …………12分
…………12分
 ,则P(
,则P( )=C
)=C …4分
…4分∴P(A)=1-

答:油罐被引爆的概率为
 …………6分
…………6分(2)射击次数ξ的可能取值为2,3,4,5,…………7分
P(ξ=2)=
 , P(ξ=3)=C
, P(ξ=3)=C ,
,P(ξ=4)=C
 , P(ξ=5)=C
, P(ξ=5)=C …………10分
…………10分故ξ的分布列为:
| ξ | 2 | 3 | 4 | 5 |
P |  |  |  |  |
Eξ=2×
 +3×
+3× +4×
+4× +5×
+5× =
= …………12分
…………12分
练习册系列答案
相关题目
 .,每次命中与否互相独立.
.,每次命中与否互相独立. ,其中
,其中 分别为甲、乙摸到的球的编号。
分别为甲、乙摸到的球的编号。



 的分布列及数学期望
的分布列及数学期望
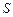 的正方形
的正方形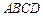 中有一个不规则的图形M,可按下面方法估计M的面积:在正方形
中有一个不规则的图形M,可按下面方法估计M的面积:在正方形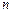 个点,若
个点,若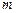 个点落入M中,则M的面积的估计值为
个点落入M中,则M的面积的估计值为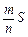 . 假设正方形
. 假设正方形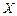 表示落入M中的点的数目.
表示落入M中的点的数目.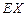 ;
; (Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间
(Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间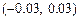 内的概率.
内的概率.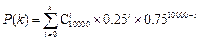
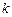
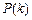
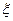 表示所选3人中女同学的人数.
表示所选3人中女同学的人数.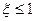 ,求共有不同选法的种数;
,求共有不同选法的种数; 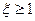 ”的概率.
”的概率. 个红球
个红球 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。 ;
; ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率; ,构造数列
,构造数列 ,使
,使
 ,记
,记 .
. 时的概率;
时的概率; 的概率.
的概率.