题目内容
将3个相同的黑球和3个相同的白球自左向右排成一排,如果满足:从任何一个位置(含这个位置)开始向右数,数到最末一个球,黑球的个数大于或等于白球的个数,就称这种排列为“有效排列”,则出现“有效排列”的概率为
- A.

- B.

- C.

- D.

B
分析:由题意知六个球由3个相同的黑球和3个相同的白球组成,自左向右排成一排全部的排法有 ,再由列举法得出“有效排列”的排法种数,由公式求出概率
,再由列举法得出“有效排列”的排法种数,由公式求出概率
解答:由意六个球由3个相同的黑球和3个相同的白球组成,自左向右排成一排全部的排法有 =20,
=20,
构成“有效排列”的有:黑黑黑白白白 黑白黑白黑白 黑白黑黑白白 黑黑白黑白白 黑黑白白黑白 共五种
所以出现“有效排列”的概率为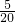 =
=
故选B
点评:本题考查等可能事件的概率,求解的关键是求出“有效排列”的种数,以及掌握求等可能事件的概率公式,本题中考查了新定义,此类题要对定义进行理解,依据定义进行运算,新定义的题是一种考查阅读能力及应用能力的一种重要题型,近几年的高考中多有出现,要好好把握其规律.
分析:由题意知六个球由3个相同的黑球和3个相同的白球组成,自左向右排成一排全部的排法有
 ,再由列举法得出“有效排列”的排法种数,由公式求出概率
,再由列举法得出“有效排列”的排法种数,由公式求出概率解答:由意六个球由3个相同的黑球和3个相同的白球组成,自左向右排成一排全部的排法有
 =20,
=20,构成“有效排列”的有:黑黑黑白白白 黑白黑白黑白 黑白黑黑白白 黑黑白黑白白 黑黑白白黑白 共五种
所以出现“有效排列”的概率为
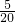 =
=
故选B
点评:本题考查等可能事件的概率,求解的关键是求出“有效排列”的种数,以及掌握求等可能事件的概率公式,本题中考查了新定义,此类题要对定义进行理解,依据定义进行运算,新定义的题是一种考查阅读能力及应用能力的一种重要题型,近几年的高考中多有出现,要好好把握其规律.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目







