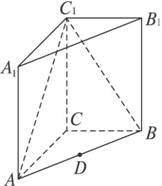
题目内容
如图,已知在侧棱垂直于底面三棱柱ABC—A1B1C1中AC=3,AB=5,cos∠CAB=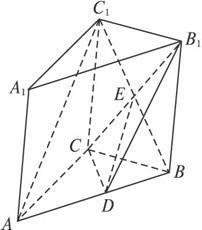
(1)求证:AC1//平面CDB1;
(2)求B1到平面A1BC1的距离.
答案:(1)证明:连结B1C交BC1于E,则E为BC1的中点,连结DE,则在△ABC1中,DE//AC1.

又DE![]() 平面CDB1,则AC1//平面CDB1.
平面CDB1,则AC1//平面CDB1.
(2)解法一:在△ABC中由余弦定理得BC=4,
∴△ABC为∠C=90°的直角三角形.
又A1A=4,∴B1BCC1为正方形.
∴A1C1⊥B1C.B1C⊥平面A1C1B,
B1到平面A1C1B的距离为B1E.∴B1E=22.
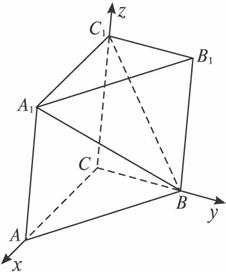
解法二:在△ABC中由余弦定理得BC=4,
∴△ABC为∠C=90°的直角三角形.
故可建立如下图所示的直角坐标系,则A1(3,0,4),B(0,4,0),C1(0,0,4),B1(0,4,4).
设n=(x,y,z)为平面A1BC1的法向量,则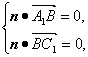
即![]()
可得n=(0,1,1),∴d=![]() =
=![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
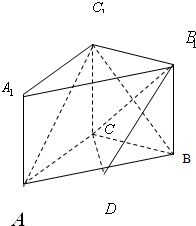 如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,
如图,已知在侧棱垂直于底面三棱柱ABC-A1B1C1中,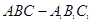 中,
中,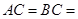
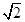 ,且
,且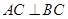 ,点
,点 是
是 中点.
中点.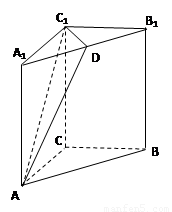
 ⊥平面
⊥平面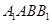 ;
;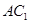 与平面
与平面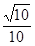 ,
,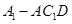 的体积.
的体积.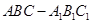 中,
中,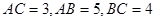 ,
,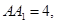 点
点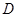 是
是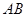 的中点。
的中点。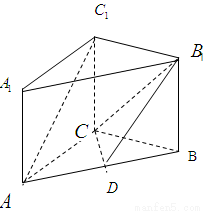

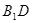 与平面
与平面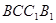 所成的角的正切值
所成的角的正切值