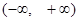题目内容
定义在R上的可导函数f(x),且f(x)图像连续,当x≠0时, 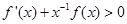 ,则函数
,则函数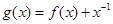 的零点的个数为( )
的零点的个数为( )
| A.1 | B.2 | C.0 | D.0或2 |
C
解析试题分析:由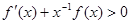 ,得
,得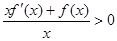 ,
,
当 时,
时,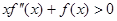 ,即
,即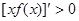 ,函数
,函数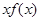 单调递增;
单调递增;
当 时,
时,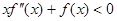 ,即
,即 ,函数
,函数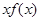 单调递减.
单调递减.
又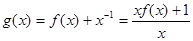 ,函数
,函数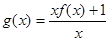 的零点个数等价为函数
的零点个数等价为函数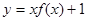 的零点个数.
的零点个数.
当 时,
时,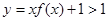 ,当
,当 时,
时,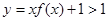 ,所以函数
,所以函数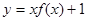 无零点,所以函数
无零点,所以函数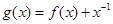 的零点个数为0个.故选C.
的零点个数为0个.故选C.
考点:根的存在性及根的个数判断;利用导数研究函数的单调性.
点评:本题考查根的存在性及根的个数的判断,涉及函数的单调性,属中档题.

练习册系列答案
相关题目
已知函数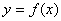 在
在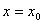 处可导,则
处可导,则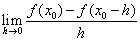 等于
等于
A.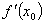 | B.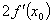 | C.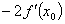 | D.0 |
若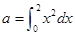 ,
, ,
,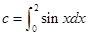 ,则
,则 、
、 、
、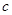 的大小关系是( )
的大小关系是( )
A.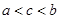 | B.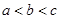 | C.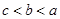 | D.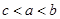 |
由曲线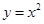 与
与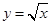 的边界所围成区域的面积为
的边界所围成区域的面积为
A.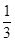 | B.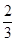 | C.1 | D.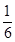 |
已知函数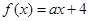 ,若
,若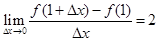 ,则实数
,则实数 的值为( )
的值为( )
A.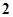 | B.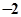 | C.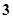 | D.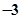 |
已知点 在曲线
在曲线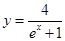 上,
上, 为曲线在点
为曲线在点 处的切线的倾斜角,则
处的切线的倾斜角,则 的取值范围为( )
的取值范围为( )
A.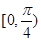 | B.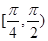 | C. | D.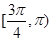 |
函数 =
=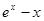 (
(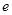
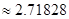 )在区间[-1,1]上的最大值是( )
)在区间[-1,1]上的最大值是( )
A.1+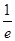 | B.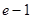 | C.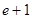 | D.1 |

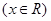 满足
满足 ,则当
,则当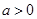 时,
时, 和
和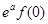 的大小关系为( )
的大小关系为( )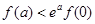 (B)
(B)
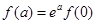 (C)
(C)
 为曲线
为曲线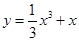 上的任意一点,在点
上的任意一点,在点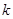 ,则
,则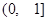 B
B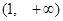 C.
C.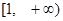 D.
D.