题目内容
已知F1、F2是双曲线
-
=1(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线的左支交于A,B两点,若△ABF2是正三角形,试求该双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
分析:利用直角三角形中含30°角所对的边的性质及其双曲线的定义、勾股定理即可得到a,c的关系.
解答:解:由△ABF2是正三角形,则在Rt△AF1F2中,有∠AF2F1=30°,
∴|AF1|=
|AF2|,又|AF2|-|AF1|=2a.
∴AF2=4a,AF1=2a,又F1F2=2c,
又在Rt△AF1F2中,|AF1|2+|F1F2|2=|AF2|2,得到4a2+4c2=16a2,∴
=3.
∴e=
=
.
∴|AF1|=
| 1 |
| 2 |
∴AF2=4a,AF1=2a,又F1F2=2c,
又在Rt△AF1F2中,|AF1|2+|F1F2|2=|AF2|2,得到4a2+4c2=16a2,∴
| c2 |
| a2 |
∴e=
| c |
| a |
| 3 |
点评:熟练掌握直角三角形中含30°角所对的边的性质及其双曲线的定义、勾股定理、离心率的计算公式等事件他的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
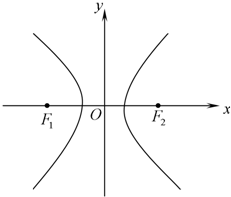
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.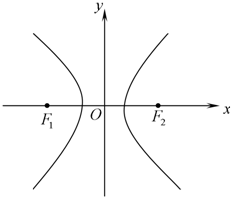
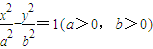 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若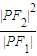 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )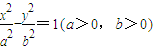 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若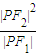 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )