题目内容
数列{an}中，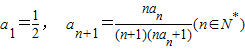
，则数列{an}的前2012项的和为 ．
【答案】分析：由已知可得，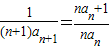
=
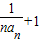即
，
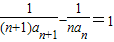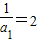，可得数列{
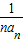}是以2为首项，以1为公差的等差数列，利用等差数列的通项公式可求
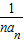，进而可求an，然后利用裂项求和即可求解
解答：解：∵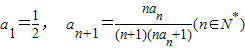
∴
=
∴
∵
∴
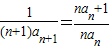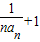
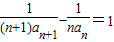
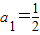
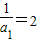
∴数列{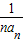
}是以2为首项，以1为公差的等差数列
∴
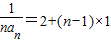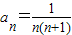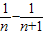
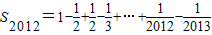=n+1
∴
=
∴
=1-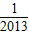
=
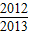
故答案为：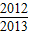
点评：本题主要考查了利用数列的递推公式求解数列的 和，解题的关键是构造等差数列求出数列的通项公式，及裂项求和方法的应用．
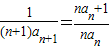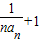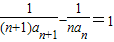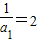=即，，可得数列{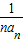}是以2为首项，以1为公差的等差数列，利用等差数列的通项公式可求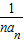，进而可求an，然后利用裂项求和即可求解解答：解：∵
∴
=∴
∵
∴
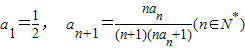
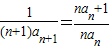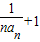
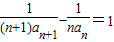
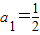
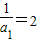
∴数列{
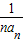}是以2为首项，以1为公差的等差数列∴
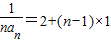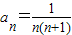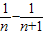
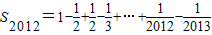=n+1∴
=∴
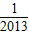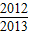
=1-=故答案为：
点评：本题主要考查了利用数列的递推公式求解数列的 和，解题的关键是构造等差数列求出数列的通项公式，及裂项求和方法的应用．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
,
,则数列的前五项为 ，猜想它的通项公式为 .
,
,则数列的前五项为 ，猜想它的通项公式为 .
，则a5=（ ）
，则a5=（ ）
，则a2+a4+a6+…+a2n+…= ．