Question

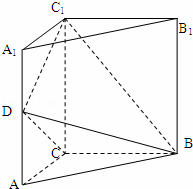
如图，三棱柱ABC﹣A₁B₁C₁中，侧棱垂直底面，∠ACB=90°，AC=BC=AA₁，D是棱AA₁的中点．

（I） 证明：平面BDC₁⊥平面BDC

（Ⅱ）平面BDC₁分此棱柱为两部分，求这两部分体积的比．

Answer 1

考点：

平面与平面垂直的判定；棱柱的结构特征；棱柱、棱锥、棱台的体积．

专题：

计算题；证明题．

分析：

（Ⅰ）由题意易证DC₁⊥平面BDC，再由面面垂直的判定定理即可证得平面BDC₁⊥平面BDC；

（Ⅱ）设棱锥B﹣DACC₁的体积为V₁，AC=1，易求V₁=××1×1=，三棱柱ABC﹣A₁B₁C₁的体积V=1，于是可得（V﹣V₁）：V₁=1：1，从而可得答案．

解答：

证明：（1）由题设知BC⊥CC₁，BC⊥AC，CC₁∩AC=C，

∴BC⊥平面ACC₁A₁，又DC₁⊂平面ACC₁A₁，

∴DC₁⊥BC．

由题设知∠A₁DC₁=∠ADC=45°，

∴∠CDC₁=90°，即DC₁⊥DC，又DC∩BC=C，

∴DC₁⊥平面BDC，又DC₁⊂平面BDC₁，

∴平面BDC₁⊥平面BDC；

（2）设棱锥B﹣DACC₁的体积为V₁，AC=1，由题意得V₁=××1×1=，

又三棱柱ABC﹣A₁B₁C₁的体积V=1，

∴（V﹣V₁）：V₁=1：1，

∴平面BDC₁分此棱柱两部分体积的比为1：1．

点评：

本题考查平面与平面垂直的判定，着重考查线面垂直的判定定理的应用与棱柱、棱锥的体积，考查分析，表达与运算能力，属于中档题．