题目内容
已知 展开式的各项依次记为a1(x),a2(x),a3(x),…,an(x),an+1(x),其中
展开式的各项依次记为a1(x),a2(x),a3(x),…,an(x),an+1(x),其中
设F(x)=a1(x)+2a2(x)+3a3(x)+…+nan(x)+(n+1)an+1(x)
(1)若a1(x),a2(x),a3(x)的系数依次成等差数列,求n的值;
(2)求证:对任意x1,x2∈[0,2],恒有
 .
.
【答案】分析:(1)利用二项展开式的通项公式,求出前三项的系数,据a1(x),a2(x),a3(x)的系数依次成等差数列,列出方程,即可求出n的值.
(2)先利用到序相加法求出F(2)-F(0)的值,利用导数判断出函数的单调性,即可得证.
解答:(1)解:∵
∴a1(x),a2(x),a3(x)的系数依次为 =1,
=1, =
= ,
, =
=
∵a1(x),a2(x),a3(x)的系数依次成等差数列,
∴
∴n=8;
(2)证明:∵F(x)=a1(x)+2a2(x)+3a3(x)+…+nan(x)+(n+1)an+1(x)= +2
+2 +…+
+…+
∴F(2)= +2
+2 +…+
+…+
设Sn= +2
+2 +…+
+…+ ,倒序可得Sn=
,倒序可得Sn= +…+2
+…+2 +
+
考虑到Cnk=Cnn-k,将以上两式相加得:2Sn=(n+2)(Cn+Cn1+Cn2…+Cnn-1+Cnn)
所以Sn=(n+2)2n-1
所以F(2)-F(0)=(n+2)2n-1-1
又当x∈[0,2]时,F'(x)≥0恒成立,从而F(x)是[0,2]上的单调递增函数,
所以对任意x1,x2∈[0,2],|F(x1)-F(x2)|≤F(2)-F(0)═(n+2)2n-1-1<(n+2)2n-1.
点评:本题考查二项式定理与数列的综合,考查等差数列,考查倒序相加法,考查学生的计算能力,属于中档题.
(2)先利用到序相加法求出F(2)-F(0)的值,利用导数判断出函数的单调性,即可得证.
解答:(1)解:∵

∴a1(x),a2(x),a3(x)的系数依次为
 =1,
=1, =
= ,
, =
=
∵a1(x),a2(x),a3(x)的系数依次成等差数列,
∴

∴n=8;
(2)证明:∵F(x)=a1(x)+2a2(x)+3a3(x)+…+nan(x)+(n+1)an+1(x)=
 +2
+2 +…+
+…+
∴F(2)=
 +2
+2 +…+
+…+
设Sn=
 +2
+2 +…+
+…+ ,倒序可得Sn=
,倒序可得Sn= +…+2
+…+2 +
+
考虑到Cnk=Cnn-k,将以上两式相加得:2Sn=(n+2)(Cn+Cn1+Cn2…+Cnn-1+Cnn)
所以Sn=(n+2)2n-1
所以F(2)-F(0)=(n+2)2n-1-1
又当x∈[0,2]时,F'(x)≥0恒成立,从而F(x)是[0,2]上的单调递增函数,
所以对任意x1,x2∈[0,2],|F(x1)-F(x2)|≤F(2)-F(0)═(n+2)2n-1-1<(n+2)2n-1.
点评:本题考查二项式定理与数列的综合,考查等差数列,考查倒序相加法,考查学生的计算能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 展开式的各项依次记为
展开式的各项依次记为 .
. .
. 的系数依次成等差数列,求
的系数依次成等差数列,求 的值;
的值; ,恒有
,恒有 .
.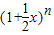 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).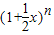 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x). 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).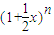 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).