题目内容
函数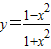
的值域是 ．
【答案】分析：先将x2用y表示出来，然后根据x2≥0建立关系式，解之即可求出y的范围，从而求出函数的值域．
解答：解：∵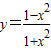
∴y（1+x2）=1-x2即（y+1）x2=1-y
当y=-1时，等式不成立
当y≠-1时，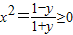
解得y∈（-1，1]
故函数的定义域为：（-1，1]
故答案为：（-1，1]
点评：本题主要考查了分式函数的值域，解这一类值域问题常常利用函数的有界性进行解题，属于中档题．
解答：解：∵
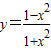
∴y（1+x2）=1-x2即（y+1）x2=1-y
当y=-1时，等式不成立
当y≠-1时，
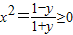解得y∈（-1，1]故函数的定义域为：（-1，1]
故答案为：（-1，1]
点评：本题主要考查了分式函数的值域，解这一类值域问题常常利用函数的有界性进行解题，属于中档题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
（2012•海淀区二模）某同学为研究函数