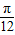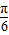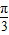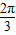题目内容
如果函数y=5tan（2x+φ）的图象关于点(
，0)中心对称，那么|φ|的最小值为（ ）
| π |
| 3 |
A．
| B．
| C．
| D．
|
∵正切函数y=tanx的对称中心为（
，0），
∵函数y=5tan（2x+φ）的图象关于点(
，0)中心对称，
∴2•
+φ=
，
∴φ=
-
π，
∴k=0时，φ=-
；k=1时，φ=-
；k=2时，φ=
，k=3时，φ=
，…
∴|φ|min=
．
故选B．
| kπ |
| 2 |
∵函数y=5tan（2x+φ）的图象关于点(
| π |
| 3 |
∴2•
| π |
| 3 |
| kπ |
| 2 |
∴φ=
| kπ |
| 2 |
| 2 |
| 3 |
∴k=0时，φ=-
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∴|φ|min=
| π |
| 6 |
故选B．
练习册系列答案
阅读快车系列答案
相关题目
中心对称，那么|φ|的最小值为
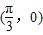中心对称，那么|φ|的最小值为（ ）
