题目内容
如果函数y=5tan(2x+φ)的图象关于点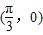 中心对称,那么|φ|的最小值为( )
中心对称,那么|φ|的最小值为( )A.
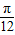
B.
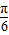
C.
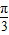
D.
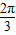
【答案】分析:利用正切函数y=tanx的对称中心为(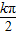 ,0),可得y=5tan(2x+φ)的对称中心,又函数y=5tan(2x+φ)的图象关于点
,0),可得y=5tan(2x+φ)的对称中心,又函数y=5tan(2x+φ)的图象关于点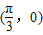 中心对称,从而可得到φ的关系式,验证即可.
中心对称,从而可得到φ的关系式,验证即可.
解答:解:∵正切函数y=tanx的对称中心为(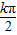 ,0),
,0),
∵函数y=5tan(2x+φ)的图象关于点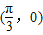 中心对称,
中心对称,
∴2•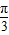 +φ=
+φ=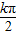 ,
,
∴φ=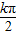 -
-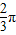 ,
,
∴k=0时,φ=-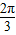 ;k=1时,φ=-
;k=1时,φ=-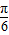 ;k=2时,φ=
;k=2时,φ=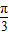 ,k=3时,φ=
,k=3时,φ=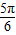 ,…
,…
∴|φ|min=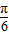 .
.
故选B.
点评:本题考查函数y=Atan(ωx+φ)的图象变换,易错点在于正切函数y=tanx的对称中心为(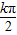 ,0),正切函数y=tanωx的对称中心受ω的影响,难点在于对“2•
,0),正切函数y=tanωx的对称中心受ω的影响,难点在于对“2•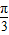 +φ=
+φ=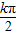 ”的理解与应用,属于中档题.
”的理解与应用,属于中档题.
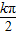 ,0),可得y=5tan(2x+φ)的对称中心,又函数y=5tan(2x+φ)的图象关于点
,0),可得y=5tan(2x+φ)的对称中心,又函数y=5tan(2x+φ)的图象关于点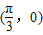 中心对称,从而可得到φ的关系式,验证即可.
中心对称,从而可得到φ的关系式,验证即可.解答:解:∵正切函数y=tanx的对称中心为(
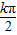 ,0),
,0),∵函数y=5tan(2x+φ)的图象关于点
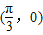 中心对称,
中心对称,∴2•
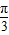 +φ=
+φ=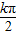 ,
,∴φ=
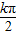 -
-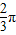 ,
,∴k=0时,φ=-
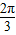 ;k=1时,φ=-
;k=1时,φ=-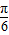 ;k=2时,φ=
;k=2时,φ=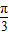 ,k=3时,φ=
,k=3时,φ=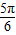 ,…
,…∴|φ|min=
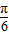 .
.故选B.
点评:本题考查函数y=Atan(ωx+φ)的图象变换,易错点在于正切函数y=tanx的对称中心为(
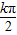 ,0),正切函数y=tanωx的对称中心受ω的影响,难点在于对“2•
,0),正切函数y=tanωx的对称中心受ω的影响,难点在于对“2•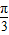 +φ=
+φ=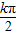 ”的理解与应用,属于中档题.
”的理解与应用,属于中档题. 
练习册系列答案
相关题目
 中心对称,那么|φ|的最小值为
中心对称,那么|φ|的最小值为


