题目内容
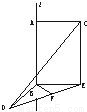
 已知直线l上有两定点A、B,线段AC⊥l,BD⊥l,AC=BD=a且AC与BD成120°角,求AB与CD间的距离.
已知直线l上有两定点A、B,线段AC⊥l,BD⊥l,AC=BD=a且AC与BD成120°角,求AB与CD间的距离.
分析:解法一:在面ABC内过B作BE⊥l于B,且BE=AC把ABEC构造成一个矩形,因为AB∥CE且平面ABEC与平面BCE交于直线EC∴AB∥平面CDE.则AB与CD的距离即为B到DE的距离,过B作BF⊥DE于F,在直角三角形BDF中,∠DBF=
×120°=60°,所以∠BDF=30°.根据在直角三角形中,30°角所对的直角边等于斜边的一半求出BF即可.
解法二;建立坐标系,则分别表示A,C,D,AB与CD的公垂线的方向向量
,利用
•
为零,
•
为零,求出
,即求出d.
| 1 |
| 2 |
解法二;建立坐标系,则分别表示A,C,D,AB与CD的公垂线的方向向量
| n |
| n |
| AB |
| n |
| CD |
| n |
解答: 解法一:在面ABC内过B作BE⊥l于B,且BE=AC,则ABEC为矩形.
解法一:在面ABC内过B作BE⊥l于B,且BE=AC,则ABEC为矩形.
∴AB∥CE.
∴AB∥平面CDE.
则AB与CD的距离即为B到DE的距离.
过B作BF⊥DE于F,易求BF=
a.
解法二:建系如图,
则A(0,0,b),C(-
a,
a,a),D(a,0,0),
设AB与CD的公垂线的一个方向向量
=(x,y,z),
利用
•
=0,
•
=0,
求出
,则d=
=
a.
 解法一:在面ABC内过B作BE⊥l于B,且BE=AC,则ABEC为矩形.
解法一:在面ABC内过B作BE⊥l于B,且BE=AC,则ABEC为矩形.∴AB∥CE.
∴AB∥平面CDE.
则AB与CD的距离即为B到DE的距离.
过B作BF⊥DE于F,易求BF=
| 1 |
| 2 |
解法二:建系如图,
则A(0,0,b),C(-
| 1 |
| 2 |
| ||
| 2 |
设AB与CD的公垂线的一个方向向量
| n |
利用
| n |
| AB |
| n |
| CD |
求出
| n |
|n•
| ||
| |n| |
| 1 |
| 2 |
点评:考查(1)要求异面直线的距离,利用平移直线的方法转化成点到线的距离.体现空间问题转化为平面问题的数学思想.
(2)构造坐标系,在坐标系中会表示一个向量,会利用
与
垂直?
•
=0.
(2)构造坐标系,在坐标系中会表示一个向量,会利用
| a |
| b |
| a |
| b |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 已知直线l上有两定点A、B,线段AC⊥l,BD⊥l,AC=BD=a且AC与BD成120°角,求AB与CD间的距离.
已知直线l上有两定点A、B,线段AC⊥l,BD⊥l,AC=BD=a且AC与BD成120°角,求AB与CD间的距离.